CHANGING THE BASE OF A LOGARITHM
CHANGING THE BASE OF A LOGARITHM
Let a, b, and x be positive real numbers such that
and
(remember
x must be greater than 0). Then
can be converted to the base
b by the formula
Let's verify this with a few examples.
Example 1: Find
to an accuracy of six decimals. Note that the
answer will be between 1 and 2 because
and
, and 7 is between
3 and 9. According to the change of logarithm rule,
can be
written
.
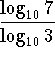When the base is 10, we can leave off the 10 in the notation.
Therefore
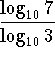can be written
. Using your calculator,
You will note that the answer is between 1 and 2.
Let's check the answer. If
, our answer is correct.
. Close
enough. Why isn't it 7 exactly? Well we rounded
to six places,
so our answer won't check exactly. If we rounded to ten places,
then when we checked the answer, it would be closer to 7 than
this answer.
Example 2: We could work the same problem by converting to the
base e. According to the change of logarithm rule,
can be written
. When the base is e, we can leave off the e in the notation
and
can be written
. Using your calculator,
You will
note that the answer is between 1 and 2.
Example 3: Find
. We know that
and
, and that 18 is between
16 and 32; therefore, we know that the exponent we are looking
for is between 4 and 5. In fact, it is closer to 4 than to 5
because 18 is closer to 16 than it is to 32.
Let's solve this problem by changing the base to 10.
can be
written
. Using your calculator,
Let's check the answer. If
, our answer is correct.
. Close
enough. Why isn't it 18 exactly? Since we rounded
to six places,
our answer won't check exactly. If we rounded to ten places,
then when we checked the answer, it would be closer to 18 than
this answer.
Example 4: We could work the problem in Example 3 by converting
to the base e. According to the logarithmic rule,
can be written
. Using your calculator,
The answer is the same as the
answer you found when you converted the base to 10.
If you would like to review more examples of changing the base
of a logarithm, click on
Example.
Work the following problems and click on answer if you want to
check your answer and review the solution.
Problem 1: Find
.
Problem 2: Find
.
Problem 3: Find
.
Problem 4: Convert
to the base 2.
S.O.S MATHematics home page