CHANGING THE BASE OF A LOGARITHM - Problem 4

Let a, b, and x be positive real numbers such that neither a nor b equals 1 (remember x must be greater than 0). Then can be converted to the base b by the formula .

Problem 4: Convert to the base 2

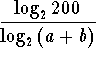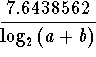
Answer: tex2html_wrap_inline58 or tex2html_wrap_inline60

Solution: Convert to the base 2.

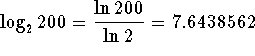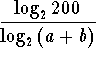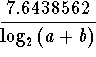The numerator can be calculated by converting the numerator to the base 10 or the base e. tex2html_wrap_inline66 . The answer tex2html_wrap_inline58 can also be written tex2html_wrap_inline60 .

Note that for this problem to be valid, the base (a + b) must be greater than zero.

If you would like to review the rules of logarithms, click on Rules.

[Previous Problem] [Menu Back to Changing Base of Logarithms]

[Algebra] [Trigonometry] [Complex Variables]

S.O.S MATHematics home page