SOLVING EXPONENTIAL EQUATIONS

To solve an exponential equation, take the log of both sides, and solve for the variable.

Example 1: Solve for x in the equation .

Solution:

Step 1: Take the natural log of both sides:

Step 2: Simplify the left side of the above equation using Logarithmic Rule 3:

Step 3: Simplify the left side of the above equation: Since Ln(e)=1, the equation reads

Ln(80) is the exact answer and x=4.38202663467 is an approximate answer because we have rounded the value of Ln(80)..

Check: Check your answer in the original equation.

Example 2: Solve for x in the equation

Solution:

Step 1: Isolate the exponential term before you take the common log of both sides. Therefore, add 8 to both sides:

Step 2: Take the common log of both sides:

Step 3: Simplify the left side of the above equation using Logarithmic Rule 3:

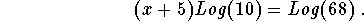
Step 4: Simplify the left side of the above equation: Since Log(10) = 1, the above equation can be written

Step 5: Subtract 5 from both sides of the above equation:

is the exact answer. x = -3.16749108729 is an approximate answer..

Check: Check your answer in the original equation. Does

Yes it does.

Example 3: Solve for x in the equation

Solution:

Step 1: When you graph the left side of the equation, you will note that the graph crosses the x-axis in two places. This means the equation has two real solutions.

Step 2: Rewrite the equation in quadratic form:

Step 3: Factor the left side of the equation:

can now be written

Step 4: Solve for x. Note: The product of two terms can only equal zero if one or both of the two terms is zero.

Step 5: Set the first factor equal to zero and solve for x: If

, then

and

and x=Ln(2) is the exact answer or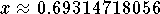

is an approximate answer.

Step 6: Set the second factor equal to zero and solve for x: If

, then

and

and x=Ln(3) is the exact answer or

is an approximate answer. The exact answers are Ln(3) and Ln(2) and the approximate answers are 0.69314718056 and 1.09861228867.

Check: These two numbers should be the same numbers where the graph crosses the x-axis.

Remark: Why did we choose the Ln in Example 3? Because we know that Ln(e) = 1.

If you would like to review another example, click on Example.

Work the following problems. If you want to review the answer and the solution, click on answer.

Problem 1: Solve for x in the equation .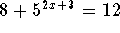

Answer

Problem 2: Solve for x in the equation tex2html_wrap_inline181 .

Answer

Problem 3: Solve for x in the equation .

Answer

Problem 4: Solve for x in the equation tex2html_wrap_inline185 .

Answer

Problem 5: Solve for x in the equation 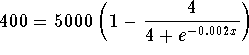tex2html_wrap_inline187 .

Answer

Problem 6: Solve for x in the equation .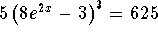

Answer

[Menu Back to Exponential Functions] [Go on to Solving Logarithmic Equations]

[Algebra] [Trigonometry] [Complex Variables]

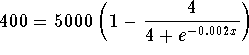S.O.S MATHematics home page