The Method of Partial Fractions

4. The bottom polynomial can be factored into . Thus we obtain

Finding the coefficients

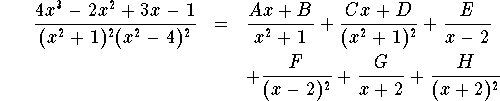
Let's consider the third problem:

Let's first multiply both sides by the least common denominator :

Then we bring the right hand side into "standard form'':

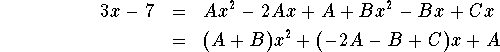
We need the left side polynomial and the right side polynomial to coincide; but two polynomials coincide if and only if all their coefficients are the same! Thus

implies the following system of linear equations:

Let's solve this system and we're done! The third equation implies A=-7, using this information in the first equation yields B=7; last not least, solving the second equation for C we obtain:

This is it. We have computed that

Remarks.

(1) The last step is "pure'' matrix algebra, so you can use any method of solving a system of linear equations you know:

• the ad-hoc method (see above)
• the Gauss elimination method
• your programmable calculator
• a computer math system

(2) Solving systems of linear equations with "pencil and paper'' is quite error-prone! You can check your answer by combining the partial fractions you obtain into the complicated fraction you started out with.

(2) The computations can be quite cumbersome. For instance, rewriting the fourth problem

using Mathematica yields the partial fraction decomposition

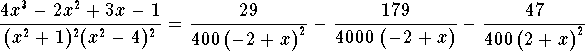
You definitely don't want to do this "by hand''!

Try it yourself!

Here are some problems you can and should do "by hand'':

1. 
2. 
3. 
4. 

Click on the problem to see the answer! Click here to continue.

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA