 SOLVING LOGARITHMIC EQUATIONS
SOLVING LOGARITHMIC EQUATIONS SOLVING LOGARITHMIC EQUATIONS
SOLVING LOGARITHMIC EQUATIONS
Note:
If you would like an in-depth review of logarithms, the rules of logarithms, logarithmic functions and logarithmic equations, click on logarithmic functions.
Solve for x in the following equation.
Problem 8.4a:
Answers:
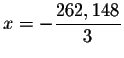
Solution:
The above equation is valid only if
![]() is valid. The term
is valid. The term
![]() is valid if
is valid if
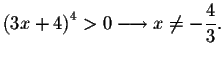 Therefore, the
equation is valid when
Therefore, the
equation is valid when
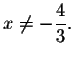 Another way of saying this is
that the domain is the set of real numbers where
Another way of saying this is
that the domain is the set of real numbers where
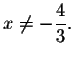
If you choose to work the problem by first removing the exponent 4, you will
lose one of the solutions because
![]() is
equivalent to
is
equivalent to
![]() only when
only when
 .
.
Covert the logarithmic equation to an exponential equation.
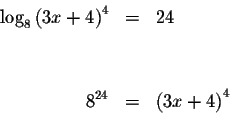
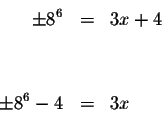
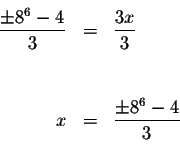


These answers may or may not be the solutions to the original equation. You must check them in the original equation, either by numerical substitution or by graphing.
Numerical Check:
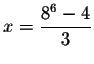 by substituting 87,380 in
the original equation for x. If the left side of the equation equals the
right side of the equation after the substitution, you have found the
correct answer.
by substituting 87,380 in
the original equation for x. If the left side of the equation equals the
right side of the equation after the substitution, you have found the
correct answer.
Left Side:

Right Side:![]()
Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 87,380 for x, then x=87,380 is a solution.
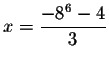 by substituting
by substituting
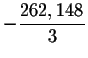 in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
Left Side:
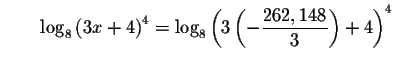

Right Side:![]()
Since the left side of the original equation is equal to the right side of
the original equation after we substitute the value
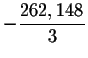 for x, then
for x, then
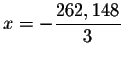 is a solution.
is a solution.
Graphical Check:
You can also check your answer by graphing
![]() (formed by subtracting the right side of the
original equation from the left side). Look to see where the graph crosses
the x-axis; that will be the real solution. Note that the graph crosses the
x-axis at 87,380 and
-87,382.66666667. This means that 87,380 and
-87,382.66666667 are the real solutions.
(formed by subtracting the right side of the
original equation from the left side). Look to see where the graph crosses
the x-axis; that will be the real solution. Note that the graph crosses the
x-axis at 87,380 and
-87,382.66666667. This means that 87,380 and
-87,382.66666667 are the real solutions.
If you have trouble graphing the function
![]() ,
graph the equivalent function
,
graph the equivalent function
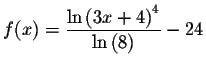 .
.
If you would like to review the solution to problem 8.4b, click on solution.
If you would like to go to the next section, click on
next.
If you would like to go back to the previous section, click on
previous.
If you would like to go back to the equation table of contents, click on
contents.
This site was built to accommodate the needs of students. The topics and problems are what students ask for. We ask students to help in the editing so that future viewers will access a cleaner site. If you feel that some of the material in this section is ambiguous or needs more clarification, or you find a mistake, please let us know by e-mail.

