
 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS

Note: If you would like a review of trigonometry, click on trigonometry.
Problem 9.4d: Solve for x in the following equation.
Answers:
There are an infinite number of solutions. The exact solutions are
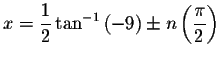 and
and
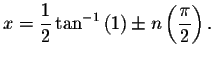
The approximate solutions are
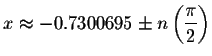 and
and

Solution:
To solve for x, you must isolate the tangent term. In this problem we do this by rewriting the original equation in an equivalent factored form.
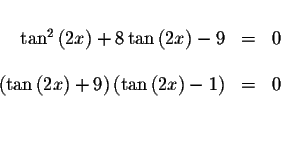
The only way that a product can equal zero is if at least one of the factors
equals zero.
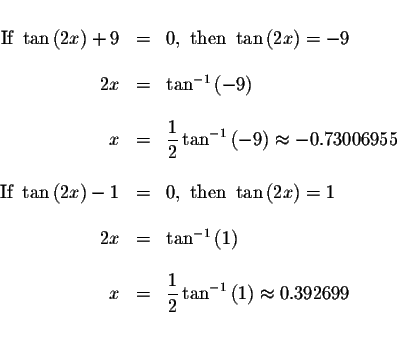
The period of tan
![]() is
is ![]() ,
and the period of tan
,
and the period of tan
![]() is
is
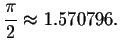
Since the period is
![]() this means that the rest of the
solutions can be found by adding or subtracting multiples of
this means that the rest of the
solutions can be found by adding or subtracting multiples of
![]() to each of the above solutions. Therefore, the solutions are
to each of the above solutions. Therefore, the solutions are
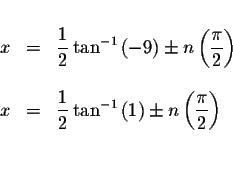
These solutions may or may not be the answers to the original problem. You much check them, either numerically or graphically, with the original equation.
Numerical Check:
Check the answer x=-0.73006955
Left Side:
![\begin{displaymath}\tan^{2}\left( 2x\right) +8\tan \left( 2x\right) -9\approx
\t...
...n \left( 2\left[
-0.73006955\right] \right) -9\approx 0\bigskip\end{displaymath}](img15.gif)
Right Side: ![]()
Since the left side equals the right side when you substitute -0.73006955for x, then -0.73006955 is a solution.
Check the answer . x=0.392699
Left Side:
![\begin{displaymath}\tan^{2}\left( 2x\right) +8\tan \left( 2x\right) -9\approx
\t...
...\tan \left( 2\left[
0.392699\right] \right) -9\approx 0\bigskip\end{displaymath}](img17.gif)
Right Side: ![]()
Since the left side equals the right side when you substitute 0.392699 for x, then 0.392699 is a solution.
Graphical Check:
Graph the equation
![]() (Formed by subtracting the right side of the original equation from the left
side of the original equation.
(Formed by subtracting the right side of the original equation from the left
side of the original equation.
Note that the graph crosses the x-axis many times indicating many solutions.
Check to see if the graph crosses at the two solutions. It does. Check also
to see if the graph crosses to the right and left of each solution by
 .
It does.
.
It does.
If you would like to go to the next section, click on Next.
If you would like to go back to the previous section, click on previous.
If you would like to go back to the equation table of contents, click on Contents.

