 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS
Note: If you would like a review of trigonometry, click on trigonometry.
Example 1: Solve for x in the following equation.
There are an infinite number of solutions to this problem. To solve for x, set the equation equal to zero and factor.
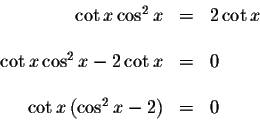
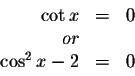
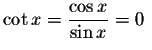 when
when ![]()
![]() when
when
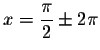 ,
and when
,
and when
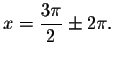
![]() when
when
![]() and
and
![]() This is
impossible because
This is
impossible because
![]()
The exact value solutions are
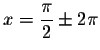 and
and
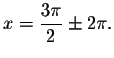 The approximate value of these solutions are
The approximate value of these solutions are
These solutions may or may not be the answers to the original problem. You much check them, either numerically or graphically, with the original
equation.
Numerical Check:
Check the answer x=1.5707963
Left Side:
Right Side:
Since the left side equals the right side when you substitute 1.5707963for x, then 1.5707963 is a solution.
Check the answer x=4.71238898
Left Side:
Right Side:
Since the left side equals the right side when you substitute 4.71238898for x, then 4.71238898 is a solution.
Graphical Check:
Graph the equation
![]() Note that the graph
crosses the x-axis many times indicating many solutions.
Note that the graph
crosses the x-axis many times indicating many solutions.
Note that it crosses at 1.5707963. Since the period is
![]() ,
it crosses again at
1.5707963+6.2831853=7.85398 and at
<tex2htmlcommentmark>
1.5707963+2(6.2831853)=14.137167, etc.
,
it crosses again at
1.5707963+6.2831853=7.85398 and at
<tex2htmlcommentmark>
1.5707963+2(6.2831853)=14.137167, etc.
Note that it crosses at
4.71238898. Since the period is
![]() ,
it crosses again at
4.71238898+6.2831853=10.99557 and at
<tex2htmlcommentmark>
4.71238898+2(6.2831853)=17.27876, etc.
,
it crosses again at
4.71238898+6.2831853=10.99557 and at
<tex2htmlcommentmark>
4.71238898+2(6.2831853)=17.27876, etc.
If you would like to test yourself by working some problems similar to this example, click on Problem.
If you would like to go to the next section, click on next.
If you would like to go back to the previous section, click on previous.
If you would like to go back to the equation table of contents, click on Contents.

