 Implicit Differentiation - Exercise 1
Implicit Differentiation - Exercise 1 Implicit Differentiation - Exercise 1
Implicit Differentiation - Exercise 1Exercise 1. Find y' if xy3 + x2y2 + 3x2 - 6 = 1.
Answer. Let us use implicit differentiation. Then we take
the derivative of the equation treating y as a function of
x. We get
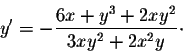
 S.O.S MATHematics home page
S.O.S MATHematics home page