Implicit Differentiation

In many examples, especially the ones derived from differential equations, the variables involved are not linked to each other in an explicit way. Most of the time, they are linked through an implicit formula, like F(x,y) =0. Once x is fixed, we may find y through numerical computations. (By some fancy theorems, we may formally show that y may indeed be seen as a function of x over a certain interval). The question becomes what is the derivative $\displaystyle \frac{dy}{dx}$ , at least at a certain a point? The method of implicit differentiation answers this concern. Let us illustrate this through the following example.

Example. Find the equation of the tangent line to the ellipse

25 x² + y² = 109

at the point (2,3). One way is to find y as a function of x from the above equation, then differentiate to find the slope of the tangent line. We will leave it to the reader to do the details of the calculations. Here, we will use a different method. In the above equation, consider y as a function of x:

25 x² + y(x)² = 109,

and use the techniques of differentiation, to get

$\begin{displaymath}\frac{d}{dx} \Big[25 x^2 + y(x)^2\Big] = 50 x + 2y \frac{dy}{dx} = 0\cdot\end{displaymath}$

From this, we obtain

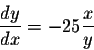
$\begin{displaymath}\frac{dy}{dx} = - 25 \frac{x}{y}\end{displaymath}$

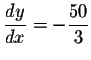which implies that $\displaystyle \frac{dy}{dx} = - \frac{50}{3}$ at the point (2,3). So the equation of the tangent line is given by

$\begin{displaymath}y - 3 = -\frac{50}{3} (x-2),\end{displaymath}$

or equivalently

3y + 50 x = 109.

You may wonder why bother if this is just a different way of finding the derivative? Consider the following example! It can be very hard or in fact impossible to solve explicitly for y as a function of x.

Example. Find y' if

$\begin{displaymath}y^4 + 4y - 3x^3 \sin(y) = 2x+1 \cdot\end{displaymath}$

This is a wonderful example of an implicit relation between xand y. So how do we find y'? Let us differentiate the above equation with respect to x where y is considered to be a function of x. We get

$\begin{displaymath}4y^3 y' + 4y' - 9x^2 \sin(y) - 3x^3\cos(y)y' = 2.\end{displaymath}$

Easy algebraic manipulations give

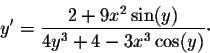
$\begin{displaymath}y' = \frac{2 + 9 x^2 \sin(y)}{4y^3 + 4 - 3x^3 \cos(y)} \cdot\end{displaymath}$

We can also find higher derivatives of y such as y'' in this manner. We only have to differentiate the above result. Of course the calculations get little more messy.

Exercise 1. Find y' if xy³ + x²y² + 3x² - 6 = 1.

Answer.

Exercise 2. Prove that an equation of the tangent line to the graph of the hyperbola

$\begin{displaymath}\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\end{displaymath}$

at the point P(x₀,y₀) is

$\begin{displaymath}\frac{x x_0}{a^2} - \frac{y y_0}{b^2} = 1\end{displaymath}$

Answer.

Exercise 3. Show that if a normal line to each point on an ellipse passes through the center of an ellipse, then the ellipse is a circle.

Answer.

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA