 Implicit Differentiation - Exercise 2
Implicit Differentiation - Exercise 2
Exercise 2. Prove that an equation of the tangent line to
the graph of the hyperbola
at the point
P(x0,y0) is
Answer. Instead of finding y explicitly as a function of
x, we will use implicit differentiation to find the slope of
the tangent line. We have
or equivalently
So the equation of the tangent line at the point
P(x0,y0) is
or equivalently
Knowing that
the equation of the tangent line becomes
[Back]
[Next]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Implicit Differentiation - Exercise 2
Implicit Differentiation - Exercise 2 Implicit Differentiation - Exercise 2
Implicit Differentiation - Exercise 2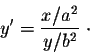
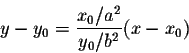
 S.O.S MATHematics home page
S.O.S MATHematics home page