 Implicit Differentiation - Exercise 3
Implicit Differentiation - Exercise 3
Exercise 3. Show that if a normal line to each point on an
ellipse passes through the center of an ellipse, then the ellipse
is a circle.
Answer. An equation of the ellipse is given by
where we assumed that (0,0) is the center. We may always do
that. Let (x0,y0) be a point on the ellipse. The slope of
the tangent line to the ellipse at this point will be obtained
through implicit differentiation. Indeed, we have
or equivalently
So the slope of the tangent line at the point (x0,y0) is
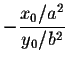 which gives the slope
of the normal line as
which gives the slope
of the normal line as
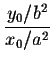 .
Hence the equation of the normal line is
.
Hence the equation of the normal line is
or equivalently
Assuming that (0,0) is on any normal line, we get
If we choose a point (x0,y0) such that
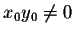 ,
we
will get
,
we
will get
a2 = b2
which clearly implies that the ellipse is a circle.
[Back]
[Next]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Implicit Differentiation - Exercise 3
Implicit Differentiation - Exercise 3 Implicit Differentiation - Exercise 3
Implicit Differentiation - Exercise 3
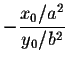 which gives the slope
of the normal line as
which gives the slope
of the normal line as
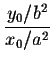 .
Hence the equation of the normal line is
.
Hence the equation of the normal line is
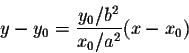
 S.O.S MATHematics home page
S.O.S MATHematics home page