 Differentiating Inverse Functions
Differentiating Inverse Functions
 Differentiating Inverse Functions
Differentiating Inverse Functions
Inverse functions are very important in Mathematics as well as in many applied areas of science. The most famous pair of functions inverse to each other are the logarithmic and the exponential functions. Other functions like the tangent and arctangent play also a major role.
In any case, let f(x) be an invertible function, with
f-1(x) as its inverse, that is
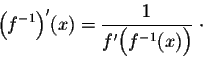
Using Leibniz's notation, the above formula becomes

Example. We will see in the coming pages that the
logarithmic function ![]() is the antiderivative of
is the antiderivative of
![]() for x > 0, with
for x > 0, with ![]() .
This
function has an inverse on
.
This
function has an inverse on
![]() ,
known to us as the
exponential function ex. So this function is differentiable
and
,
known to us as the
exponential function ex. So this function is differentiable
and
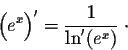
 ,
hence
,
hence

Example. Rational Powers. For x > 0, and any
natural numbers n and m, we have
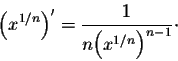
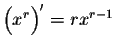 is also
valid for r=1/n, for
is also
valid for r=1/n, for
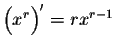 is
valid even when r is a rational number. In particular combined
with the chain rule, we get
is
valid even when r is a rational number. In particular combined
with the chain rule, we get
Example. We have
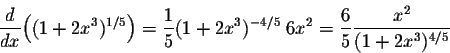
The following example discusses the above ideas for trigonometric functions.
Example. Consider the tangent function ![]() on the
interval
on the
interval
 .
Then
.
Then ![]() has an
inverse function
has an
inverse function
![]() known as the arctangent
function, which we prefer to denote by
known as the arctangent
function, which we prefer to denote by
![]() .
Since
.
Since
 ,
then
,
then

Exercise 1. Compute
Exercise 2. Compute
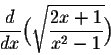
![]()
 S.O.S MATHematics home page
S.O.S MATHematics home page
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA