Differentiation and Continuity

In one of our previous pages, we have seen that if f'(x₀) exists, then for x close to x₀, we have

$$f(x) \approx f(x_0) + f'(x_0)(x-x_0)\;.$$

This is the "linear approximation" done via the tangent line. Obviously this implies

$$\lim_{x \rightarrow x_0} f(x) = f(x_0),$$

which means that f(x) is continuous at x₀. Thus there is a link between continuity and differentiability: If a function is differentiable at a point, it is also continuous there. Consequently, there is no need to investigate for differentiability at a point, if the function fails to be continuous at that point.

Note that a function may be continuous but not differentiable, the absolute value function at x₀=0 is the archetypical example.

This relationship between differentiability and continuity is local. But a global property also holds. Indeed, let f(x) be a differentiable function on an interval I. Assume that f'(x) is bounded on I, that is there exists M >0 such that

$$\vert f'(x)\vert \leq M,\;\;\mbox{for any $x \in I$.}$$

The Mean Value Theorem will then imply that

$$\vert f(x) - f(y)\vert \leq M \vert x-y\vert\;,$$

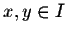for any $x, y \in I$. This is the definition of Lipschitz continuity. In other words, if f'(x) is bounded then f(x)is a Lipschitzian function. Conversely, it is also true that Lipschitzian functions have bounded first derivatives, when they exist. Since Lipschitzian functions are uniformly continuous, then f(x) is uniformly continuous provided f'(x) is bounded.

Nevertheless, a function may be uniformly continuous without having a bounded derivative. For example, 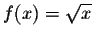$f(x) = \sqrt{x}$ is uniformly continuous on [0,1], but its derivative is not bounded on [0,1], since the function has a vertical tangent at 0.

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA