The Geometric Series

Introduction

Suppose someone offers you the following deal: You get $1 on the first day, $0.50 the second day, $0.25 the third day, and so on. For a second, you might dream about infinite riches, but adding some of the numbers on your calculator will soon convince you that this is an offer for about $2.00, spread out over quite some time.

The process of adding infinitely many numbers is at the heart of the mathematical concept of a numerical series.

Let's see why the deal above amounts to just $2.00. Let s denote the sum of the series just considered:

Let's multiply both sides by 1/2

and subtract the second line from the first. All terms on the right side except for the 1 will cancel out! Bingo:

We have shown that

One also says that this series converges to 2.

Let's play the same game for a general q instead of 1/2:

multiply both sides by q

then, subtract the second line from the first:

The series

is called the geometric series. It is the most important series you will encounter!

Example:

Find the sum of the series

First, factor out the 5 from upstairs and a 2 from downstairs:

.

The series in the parentheses is the geometric series with , but the first term, the "1" at the beginning is omitted. Thus, the series sums up to

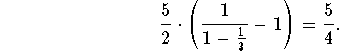
N.B. There is a slightly slicker way to do this. Do you see how?

Try it yourself!

Find the sum of the series

Click here for the answer or to continue.

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA