 Tests of Convergence
Tests of Convergence Tests of Convergence
Tests of Convergence

It is very easy to see that a simple improper integral may be very hard to decide whether it is convergent or divergent. For example, the improper integral
![]()
is hard to study since it is very difficult to find an antiderivative
of the function 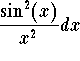 . The tests of
convergence are very useful tools in handling such improper integrals.
Unfortunately some improper integrals fails to fall under the scope of
these tests but we will not deal with them here.
. The tests of
convergence are very useful tools in handling such improper integrals.
Unfortunately some improper integrals fails to fall under the scope of
these tests but we will not deal with them here.
Recall the p-Test: Regardless of the value of the number p, the improper integral
![]()
is always divergent. Moreover, we have
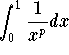 is
convergent if and only if p <1
is
convergent if and only if p <1
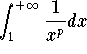 is
convergent if and only if p >1
is
convergent if and only if p >1
Note that one may generalize this test to include the following improper integrals
![]()
The conclusion is similar to the above one. Indeed we have
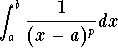 is
convergent if and only if p <1
is
convergent if and only if p <1
 is
convergent if and only if p <1
is
convergent if and only if p <1
Comparison Test Let f(x) and g(x) be two functions defined on [a,b] such that
![]()
for any ![]() . Then we have
. Then we have
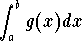 is convergent, then
is convergent, then  is convergent.
is convergent.
 is divergent, then
is divergent, then 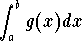 is divergent.
is divergent.
Example. Decide on the convergence or divergence of
![]()
Answer. We have for ![]()
![]()
The p-Test implies that the improper integral 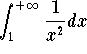 is convergent. Hence the Comparison
test implies that the improper integral
is convergent. Hence the Comparison
test implies that the improper integral
![]()
is convergent.
We should appreciate the beauty of these tests. Without them it would
have been almost impossible to decide on the convergence of this
integral.
Before we get into the limit test, we need to recall the following:
we will say and write ![]() when
when ![]() if and
only if
if and
only if
![]()
Limit test Let f(x) and g(x) be two positive functions
defined on [a,b]. Assume that both functions exhibit an improper
behavior at a and ![]() when
when ![]() , then we have
, then we have
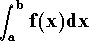 is convergent if and only if
is convergent if and only if 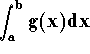 is convergent.
is convergent.
This statement is still valid whether a is a finite number or infinite or if the improper behavior is at b.
Example. Establish the convergence or divergence of
![]()
Answer. Clearly this integral is improper since the domain is unbounded (Type II). Moreover since the function 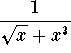 is unbounded at 0, then we also have an improper behavior at 0. First we must split the integral and write
is unbounded at 0, then we also have an improper behavior at 0. First we must split the integral and write
![]()
First let us take care of the integral 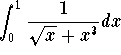 . Since
. Since
![]()
when ![]() , and (because of the p-test) the integral
, and (because of the p-test) the integral
![]()
is convergent, we deduce from the limit test that
![]()
is convergent. Next we investigate the integral 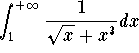 . Since
. Since
![]()
when ![]() , and (because of the p-test) the integral
, and (because of the p-test) the integral
![]()
is convergent, we deduce from the limit test that
![]()
is convergent. Therefore, the improper integral
![]()
is convergent.
Remark. One may notice that in the above example, we only used the limit test combined with the p-test. But we should keep in mind that it is not the case in general. The next example shows how the use of other tests is more than useful.
Example. Establish the convergence or divergence of
![]()
Answer. Again it is easy to see that we have an improper behavior at both 0 and ![]() . Hence we must split the integral and write
. Hence we must split the integral and write
![]()
The integral 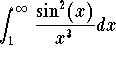 is easy to take care of since we have
is easy to take care of since we have
![]()
and because 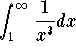 is convergent (by the p-test), the basic comparison test implies that
is convergent (by the p-test), the basic comparison test implies that
![]()
is convergent. Next we take care of the integral 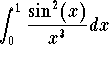 . Here we use the limit test. Indeed, since
. Here we use the limit test. Indeed, since ![]() when
when ![]() , then we have
, then we have
![]()
Because 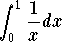 is divergent (by the p-test), then the limit test implies that the integral
is divergent (by the p-test), then the limit test implies that the integral
![]()
is divergent. Conclusion the improper integral
![]()
is divergent.
Remark. One may argue that the above example is in fact not a good one to illustrate the use of different tests. Since if we have showed first that the integral
![]()
is divergent via the limit test, then we do not need to take care of the other integral and conclude to the divergence of the given integral. A very good point. Now consider the improper integral
![]()
and show that in this case the integral is convergent. Let us point out that the trigonometric functions are very bad when it comes to look at what is happening at ![]() . Hence the limit test is absolutely not appropriate to use...
. Hence the limit test is absolutely not appropriate to use...
Example. Establish the convergence or divergence of
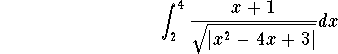
Answer. This is clearly not an improper integral of Type II. Let us check if it is of Type I. First notice that ![]() . Hence the function is unbounded at x=1 and x=3 (you must check it by taking the limit.. left as an exercise). Since 3 is between 2 and 4, we deduce that the integral is improper and the only bad point is 3. Hence we must split the integral to get
. Hence the function is unbounded at x=1 and x=3 (you must check it by taking the limit.. left as an exercise). Since 3 is between 2 and 4, we deduce that the integral is improper and the only bad point is 3. Hence we must split the integral to get
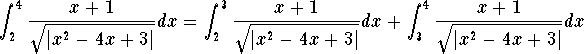
Let us take care of the integral . It is easy to see that when ![]() , then we have
, then we have
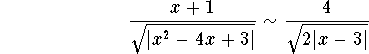
The p-test implies that the integral

is convergent. Hence by the limit test we conclude that the integral
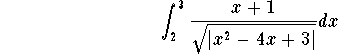
is convergent. Using the same arguments, we can show that the integral
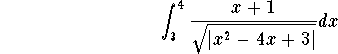
is also convergent. Therefore the integral
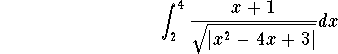
is convergent.
Note that all the tests so far are valid only for positive functions. One may then wonder what happens to improper integrals involving non positive functions. A partial answer is given by the Absolute Convergence tests.

 S.O.S MATHematics home page
S.O.S MATHematics home page 
Tue Dec 3 17:39:00 MST 1996