Indeterminate Quotient Forms Indeterminate Quotient Forms
Indeterminate Quotient Form 
May be the most natural indeterminate form is the quotient
of two small numbers or .
Equivalently another natural indeterminate form is the quotient
of two large numbers or 
. In both cases, it is very easy to convince oneself that
nothing can be said, in other words we have no conclusion. It is very
common to see students claiming 
.
We hope this page will convince some that it is not the case.
Hôpital's Rule: Though this rule was named after Hôpital, it is Bernoulli who did discover it in the early 1690s. This rule answers partially the problem stated above. Indeed, let f(x) and g(x) be two functions defined around the point a such that
Then we have
Next we take the ratio function 
. Do
any needed algebra and then find its limit. Hôpital's rule states
that if
then we have
Remark. Note that if
then you can use Hôpital's rule for the ratio function , by looking for
In other words, there is no limit where to stop.
Example. Find the limit
Answer. We have 
. Hence
Clearly we are in full swing to use Hôpital's rule. We have
Since
Therefore we have
Example. Fint the limit
Answer. We have
Hence we can use Hôpital's rule. Since 
and
, we have
So it is clear that we need to use Hôpital's rule another time. But since we proved in the example above
we conclude that
Therefore, we have
Remark. The above examples have a wonderful implication.
Indeed, the first example implies that when 
then
. The second example implies that when then
.
Example. Fint the limit
Answer. Set 
and 
.
We have f(0) = g(0) = 0. So we have all assumptions satisfied to
use Hôpital's rule. We have
Clearly we have
So we use Hôpital's rule again. Set 
and
. Then we have
Again we have
In fact another use of Hôpital's rule makes the functions involved
even more complicated. So what do we do in this case? A partial
answer is given but the use of Taylor Polynomials.
Taylor Polynomial's Technique. First recall the assumptions of the original problem: let f(x) and g(x) be two functions defined around the point a such that
Using Taylor Polynomials, we get around a (that is 
)
and
where n and m are natural numbers. Since f(a) = g(a) =0, we get
and
But we may have the next derivatives also equal to 0 at a. Hence we are sure that there exist two natural numbers N and M such that
and
when . This clearly implies
So the job is over. Indeed, it is now clear that the limit
is not a problem and depends on the natural numbers N and M.
Before we do any example showing the power behind this technique,
recall that one may use all the properties of Taylor Polynomials.
Example. Fint the limit
Answer. First we consider the basic functions which generate the
functions involved in this limit, that is 
and 
.
Next we write the Taylor Polynomials of these functions
and
Note that if more terms are needed, we will come back and put the next terms. Using properties of Taylor Polynomials, we get
and
Hence we have
Therefore, we have
One should appreciate the beauty and power behind this technique in
comparing the above calculations with the ones done under Hôpital's
rule.
Summary. If you go back to the above example, the calculations suggest the following steps to follow when using Taylor Polynomials
Example. Find
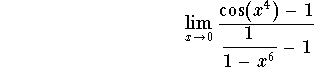
Answer. We have
and
So we can use Hôpital's rule but we will use Taylor polynomial's
technique instead. The basic functions involved are and 
. Taylor Polynomials of these functions are
and
Hence we have
and
Therefore we have
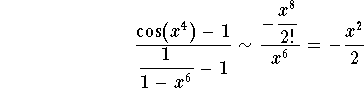
which implies
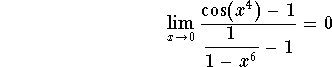
S.O.S MATHematics home page
Tue Dec 3 17:39:00 MST 1996