Other Indeterminate Quotient FormsOther Indeterminate Quotient Forms
We have discussed the indeterminate quotient form 
. But there some indeterminate quotient forms similar to
this one. Indeed, since
then one can see that the indeterminate quotient forms
as well as the indeterminate forms
may be easily converted to the indeterminate quotient form . So first notice that Hôpital's rule is still valid
when dealing with the indeterminate quotient form 
. Also worth to mention that the point
a may be finite or infinite, Hôpital's rule still applies.
Example. Find the limit
Answer. Fix 
. We have
Hence
We will use Hôpital's rule. We have
So clearly we will keep to use Hôpital's rule n-times to get to the function
Since
Therefore, we have
Note that this limit implies that, though both functions are very
large when 
, the exponential function 
is more
powerful than the power function 
(in fact more powerful than any
polynomial function). We will write
Example. Find the limit
Answer. Fix 
. We have
Hence
We will use Hôpital's rule. We have
Hence we have
which implies
Clearly this example implies that
Putting the two examples together we conclude that
when .
The indeterminate forms 
The main idea behind these indeterminate forms is to transform 0 into
(the 
depends on whether we have 0+ or
0-), or transform 
into 
.
This will lead to the indeterminate quotient forms
Practically, you will be given a product f(x)g(x) where one function
goes to 0 while the other one goes to . So you will use
the following algebraic manipulations
Example. Find the limit
Answer. We have
Hence
Rewrite the given expression into
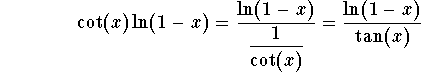
Computing the limit we will find
Here we have a choice. We may use Hôpital's rule or Taylor Polynomials. In any case, Hôpital's rule is not bad to use in this case. Indeed, we have
Since
we conclude that
Note that when 
, we have
and
which imply
May be this is easier, what do you think???
Example. Find the limit
Answer. We have again
We will ask you to check that whether you take
or
The calculations are not easy. Here let us show how some tricks may help. First switch from x into t = 1/x. We will have
Note that 
when 
. Next, we
use
(when 
), to get
We already proved that
Therefore, we have
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
