 Techniques of Integration: Substitution
Techniques of Integration: Substitution

Many integrals are hard to perform at first hand. A smart idea
consists in ``cleaning'' them through an algebraic substitution which
transforms the given integrals into easier ones. Let us first explain
how the substitution technique works.
- 1
- Write down the given integral

- 2
- Come up with a substitution u = u(x).
- 3
- Ideally you may want to find the inverse function of u(x),
meaning that you will find x = x(u).
- 4
- Differentiate to find dx = x'(u) du.
- 5
- Back to the given integral and make the appropriate
substitutions
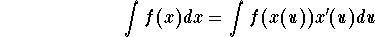
- 6
- Check after algebraic simplifications that the new integral
is easier than the initial one. Otherwise, go back to step 2 and come
up with another substitution.
- 7
- Do not forget that the answer to
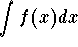 is a function of x. Therefore once you have finished doing all your
calculations, you should substitute back to the initial variable x.
is a function of x. Therefore once you have finished doing all your
calculations, you should substitute back to the initial variable x.
Remarks.
- 1
- In general, if the substitution is good, you may not need to
do step 3. Indeed, from u= u(x), differentiate to find
du=u'(x)dx. Then substitute the new variable u into the integral
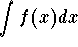 . You should make sure that the old variable x has
disappeared from the integral.
. You should make sure that the old variable x has
disappeared from the integral.
- 2
- A better substitution is sometimes hard to find at first
hand. Therefore we do not recommend spending a lot of time in step 2
trying to find it. After a while you may start to have a good feeling
for the best substitution.
- 3
- If you are given a definite integral
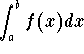 , nothing will change except in step 5 you will have to
replace a and b also, that is
, nothing will change except in step 5 you will have to
replace a and b also, that is

In this case, you will never have to go back to the initial variable x.
The following examples illustrate cases in
which you will be required to use the substitution technique:

[Calculus]
[Integration
By Parts]
[Integration
of Rational Functions]
[Geometry]
[Algebra]
[Trigonometry ]
[Differential Equations]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Techniques of Integration: Substitution
Techniques of Integration: Substitution Techniques of Integration: Substitution
Techniques of Integration: Substitution
![]()
![]()
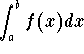 , nothing will change except in step 5 you will have to
replace a and b also, that is
, nothing will change except in step 5 you will have to
replace a and b also, that is
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page 