 The Radius of Convergence
The Radius of Convergence The Radius of Convergence
The Radius of Convergence
The partial sums increase, because all the ![]() 's were assumed to be positive.
's were assumed to be positive.
If on the other hand a series satisfies--for some q>1-- the condition
![]()
then the series will diverge; it will go "off to infinity''.
Draw a picture similar to the one on the previous page to convince yourself that this is what will happen!
|
|
|
![]()
We want to find out for what values of x the series converges. If we view this power series as a series of the form
![]()
then ![]() ,
, ![]() ,
, ![]() and so forth.
The general term will have the form
and so forth.
The general term will have the form
![]()
(Plug in ![]() to see that this formula works!)
Consequently the ratios are given by
to see that this formula works!)
Consequently the ratios are given by
![]()
Since
![]()
we obtain
![]()
What's next? Do you remember the question we are trying to answer? For what values of x does the power series converge! The ratio test tells us now that the series will converge as long as |x|<1. It also tells us that the series will diverge for |x|>1. That gives us a pretty complete picture about what's going on:
The biggest interval (it is always an interval!) where a power series is converging is called interval of convergence of the power series. The interval of convergence is always centered at the center of the power series. It is customary to call half the length of the interval of convergence the radius of convergence of the power series. In our example, the center of the power series is 0, the interval of convergence is the interval from -1 to 1 (note the vagueness about the end points of the interval), its length is 2, so the radius of convergence equals 1.
![]()
![]()
will do the job for ![]() . Since we will be taking the limit as n goes to infinity, the odd ``5'' at the beginning is of no consequence!
. Since we will be taking the limit as n goes to infinity, the odd ``5'' at the beginning is of no consequence!
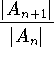 . Don't forget the absolute values!
. Don't forget the absolute values!
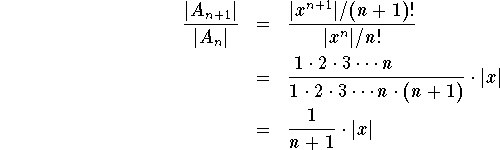
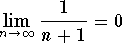 , in our case
, in our case
![]()
for all x.
Thus the interval of convergence is the interval ![]() .
The radius of convergence in this case is said to be
.
The radius of convergence in this case is said to be ![]() .
.
![]()
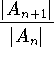 .
.
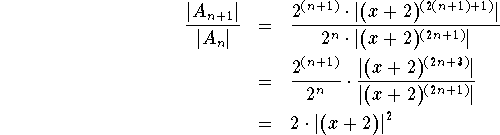
![]()
![]()
Bingo! The radius of convergence in this case is ![]() .
The interval of convergence is the interval from
.
The interval of convergence is the interval from 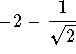 to
to 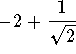 .
.
Find the radii of convergence of the following power series:
Click on the problem to see the answer. Click here to continue.