 The Ratio Test
The Ratio Test The Ratio Test
The Ratio TestThis problem is slightly trickier. If you have trouble finding the general term of the series, try the following: Ask, what happens as you move from one term to the next:
Upstairs we multiply by 2 and by x, downstairs we multiply by 3 and replace n by n+1 (this really means we multiply the term by n and divide by n+1). Thus the absolute ratio will be given by
![]()
More formally, the general term of the series has the form
![]()
leading to the same absolute ratio:
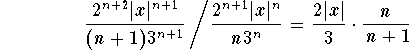
Thus the limit of the absolute ratios is given by:
![]()
The series will converge as long as 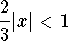 (the series will diverge when
(the series will diverge when 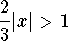 ).
).
Consequently, the radius of convergence equals ![]() ;
the series will converge in an interval from
;
the series will converge in an interval from ![]() to
to ![]() .
.
It is actually easier to find the radius of convergence when one uses the summation notation for the series. The general term is then already given!