Differential Equations Practice Exams

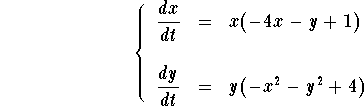
Answers

Problem 1. Consider the system

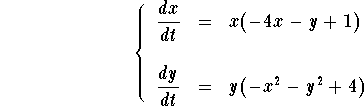
Draw the nullclines and find all equilibrium points. Determine the fate of the solutions with initial conditions

Problem 2. Find the solution of

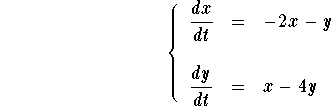
with the initial condition

Problem 3. Find the solution of

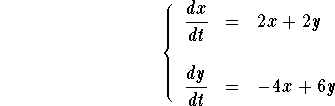
with the initial condition

Problem 4. Consider the system

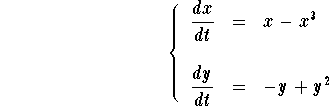
Find the equilibrium points. Find the linearized system at these points and discuss the behavior of the solutions at these points. Determine if the equilibrium points are sinks, saddles, sources, and so on...

Answers.

Answer to Problem 1. Let us find the x-nullclines and y-nullclines.

x-nullclines: We must have

which is equivalent to x = 0 or -4x-y+1 = 0.

y-nullclines: We must have

which is equivalent to y = 0 or (which is the equation of a circle centered at (0,0)).

The critical points are the intersection between the x-nullclines and y-nullclines. Hence the equilibrium points are

See the figure below for more details about the nullclines and the solutions.

1.

The solution with initial condition (1,1) goes up and left. It dies at the equilibrium point (0,2).

2.

The solution with initial condition (0,1) goes up. Indeed, it is easy to check that there are solutions which lives on the line x=0. Since this initial condition is on this line, the entire solution will stay on the line. When , the solution dies at the equilibrium point (0,2).

1.

The solution with initial condition (1,-1) goes down and left. It dies at the equilibrium point

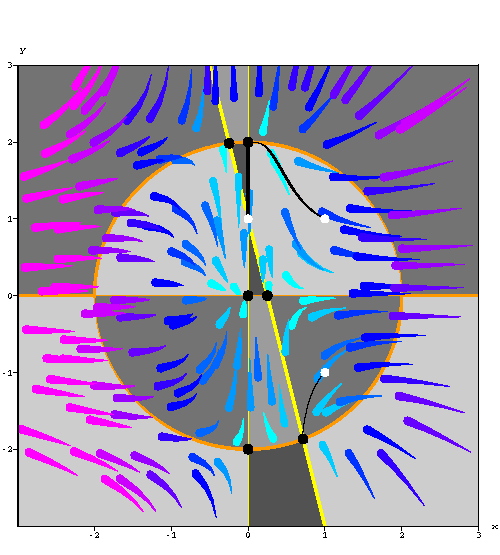Answer to Problem 2. The matrix coefficient is

The characteristic equation is

Its roots are : -3 and -3 (-3 is a double root). An eigenvector associated to -3, is

We may choose

The general solution is

where

satisfies

This gives . Hence the vector

will do (here we took ). Hence the general solution is

The initial condition Y(0) = (1,0) gives

This implies and . Therefore the solution to the initial condition is

Answer to Problem 3. The matrix coefficient is

The characteristic equation is

Its roots are

(these are complex roots). An eigenvector associated to 4 + 2i, is

We may choose

WE need the real part and imaginary part of

Easy calculations give

where

and

The general solution is

The initial condition Y(0) = (1,1) gives

which yields

This implies and . Therefore the solution to the initial condition is

Answer to Problem 4. Let us find the x-nullclines and y-nullclines.

x-nullclines: We must have

which is equivalent to x = 0 or . This gives

y-nullclines: We must have

which is equivalent to y = 0 or y = 1.

The critical points are the intersection between the x-nullclines and y-nullclines. Hence the equilibrium points are

In order to find the linearized system at these points, we must find the Jacobian of the system which is

Therefore, we have

At (0,0)

The eigenvalues are 1 and -1. Therefore, (0,0) is a saddle.

At (0,1)

The eigenvalues are 1 (which is double). Therefore, (1,1) is a source.

At

The eigenvalues are -1 and -2. Therefore, is a sink.

At

The eigenvalues are 1 and -2. Therefore, is a saddle.

See the figure below for more details on the behavior of some solutions.

[Next Exam] [Calculus] [CyberExam]

S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
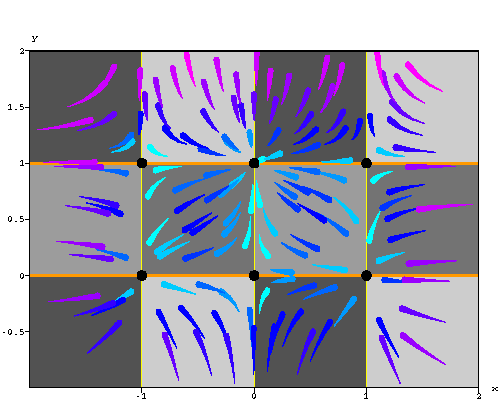Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA