 Population Dynamics: Answer to Example 2
Population Dynamics: Answer to Example 2  Population Dynamics: Answer to Example 2
Population Dynamics: Answer to Example 2

Example: The fox squirrel is a small mammal native to the Rocky Mountains. These squirrels are very territorial. Note the following observations:
![]() .
.
Answer:
![]()
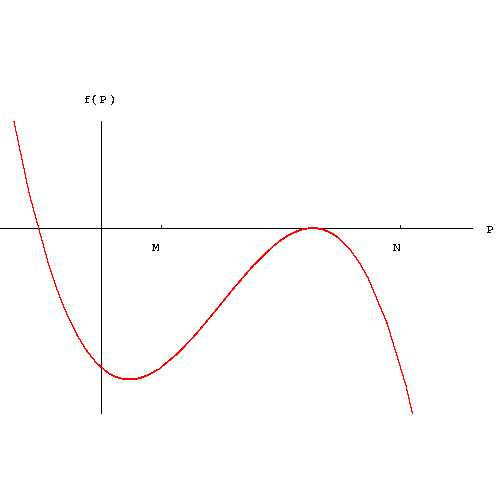
Clearly, we have P=0, P=N, and P=M. Using the graph of
![]() ,
,
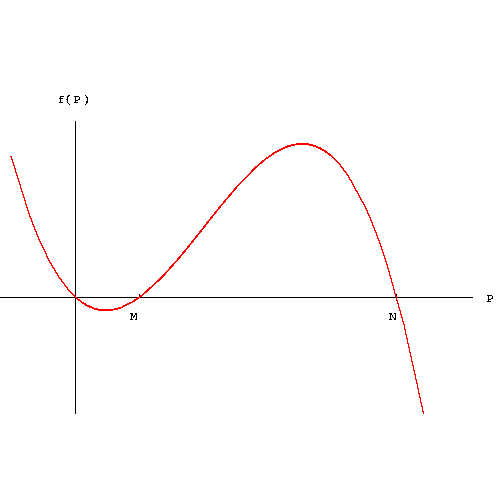 |
we get the phase-line of the equilibrium points,
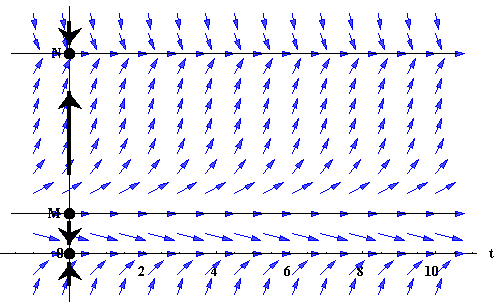 |
We conclude that P=0 and P=N are sinks, while P=M is a source.
 |
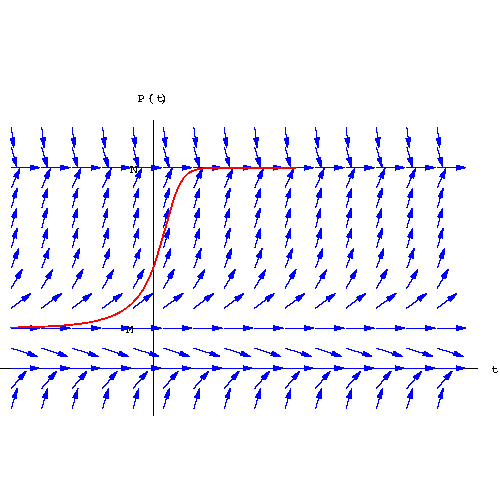 |
![]() ,
,
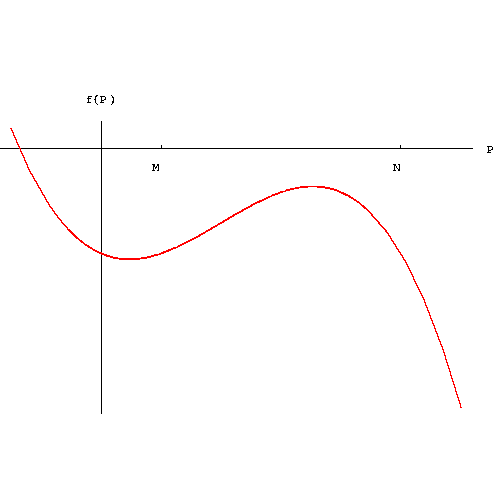
where E > 0. Clearly, the graph of the function
![]()
can be obtained by shifting the graph of
![]()
down E-unit along the vertical axis. Clearly we have three cases
according to the value of E and the value of f at the local maximum
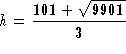 :
:
 |
 |
 |
![]()
Clearly, the bifurcation is happening when E=f(h).

 S.O.S MATHematics home page
S.O.S MATHematics home page 