 Method of Undetermined Coefficient or Guessing Method
Method of Undetermined Coefficient or Guessing Method  Method of Undetermined Coefficient or Guessing Method
Method of Undetermined Coefficient or Guessing Method

This method is based on a guessing technique. That is, we will guess
the form of ![]() and then plug it in the equation to find it. However,
it works only under the following two conditions:
and then plug it in the equation to find it. However,
it works only under the following two conditions:
![]()
where P(x) and L(x) are
polynomial functions.
Note that we may assume that g(x) is a sum
of such functions (see the remark below for more on this).
![]()
where a, b and c are constants and
![]()
where ![]() is a polynomial function with degree n. Then
a particular solution
is a polynomial function with degree n. Then
a particular solution ![]() is given by
is given by
![]()
where
![]() ,
,
where the constants ![]() and
and ![]() have to be determined. The power
s is equal to 0 if
have to be determined. The power
s is equal to 0 if ![]() is not a root of the
characteristic equation. If
is not a root of the
characteristic equation. If ![]() is a simple root, then
s=1 and s=2 if it is a double root.
is a simple root, then
s=1 and s=2 if it is a double root.
Remark: If the nonhomogeneous term g(x) satisfies the following

where ![]() are of the forms cited above, then we split the
original equation into N equations
are of the forms cited above, then we split the
original equation into N equations
![]()
then find a particular solution ![]() . A particular solution to the
original equation is given by
. A particular solution to the
original equation is given by

Summary:Let us summarize the steps to follow in applying this method:
where
where
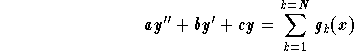 ,
, ![]() or
or ![]() , where
, where ![]() is a polynomial function
with degree n, then split this equation into N equations
is a polynomial function
with degree n, then split this equation into N equations
![]() ;
; ![]() , and
find its roots;
, and
find its roots;
![]() . Compare this
number to the roots of the characteristic equation found in previous step.
. Compare this
number to the roots of the characteristic equation found in previous step.
In other words, s measures how many times ![]() is not one of the roots, then set
s = 0;
is not one of the roots, then set
s = 0;
![]() is one of the two distinct
roots, set s = 1;
is one of the two distinct
roots, set s = 1;
![]() is equal to both root (which
means that the characteristic equation has a double root), set s=2.
is equal to both root (which
means that the characteristic equation has a double root), set s=2.
![]() is
a root of the characteristic equation;
is
a root of the characteristic equation;
![]()
![]()
![]() and
and ![]() by plugging
by plugging ![]() into the
equation
into the
equation
![]()
![]() are found, then the
particular solution of the original equation is
are found, then the
particular solution of the original equation is


 S.O.S MATHematics home page
S.O.S MATHematics home page 