Nonlinear Second Order Differential Equations
Nonlinear Second Order Differential Equations
In general, little is known about nonlinear second order differential equations
,
but two cases are worthy of discussion:
Let v = y'. Then the new equation satisfied by v is
This is a
first order differential equation. Once v is found its integration gives the function y.
Example 1: Find the solution of
Solution: Since y is missing, set v=y'. Then, we have
This is a first order linear differential equation. Its resolution gives
Since v(1) = 1, we get 
. Consequently,
we have
Since y'=v, we obtain the following equation after integration
The condition y(1) = 2 gives 
.
Therefore, we have
Note that this solution is defined for x > 0.
Let v = y'. Since
we get
This is again a first order differential equation. Once v is found then we can get y through
which is a
separable equation. Beware of the constants solutions.
Example 2: Find the general solution of the equation
Solution: Since the variable x is missing, set v=y'. The formulas above lead to
This a first order separable differential equation. Its resolution gives
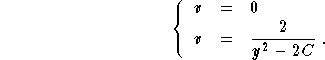
Since 
, we get y' = 0 or
Since this is a separable first order differential equation, we get, after resolution,
,
where C and 
are two constants. All the solutions of our
initial equation are
Note that we should pay special attention to the constant solutions when solving any separable equation. This may be source of mistakes...
S.O.S MATHematics home page 