


Let us look (again) at the example
We want to illustrate how to find power series solutions for a second-order linear differential equation.
The generic form of a power series is
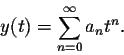
As in other techniques for solving differential equations, once we have a "guess" for the solutions, we plug it into the differential equation.
Recall from the previous section that
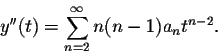
Plugging this information into the differential equation we obtain:
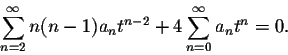
Our next goal is to simplify this expression such that only one summation sign "![]() " remains. The obstacle we encounter is that the powers of both sums are different, tn-2 for the first sum and tn for the second sum. We make them the same by shifting the index of the first sum by 2 units to obtain
" remains. The obstacle we encounter is that the powers of both sums are different, tn-2 for the first sum and tn for the second sum. We make them the same by shifting the index of the first sum by 2 units to obtain

Now we can combine the two sums as follows:

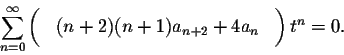
Theorem. A power series is identically equal to zero if and only if all of its coefficients are equal to zero.
This theorem applies directly to our example: The power series on the left is identically equal to zero, consequently all of its coefficients are equal to 0:
Solving these equations for the "highest index" n+2, we can rewrite
as
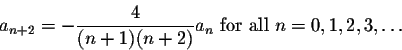
Recall that
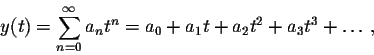

How can we evaluate the next coefficient a2? Let us read our recurrence relations for the case n=0:
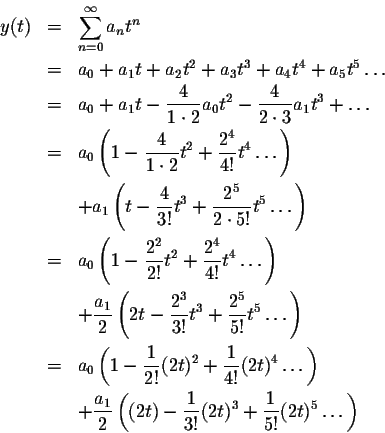
Of course the power series inside the parentheses are the familiar functions ![]() and
and ![]() :
:
The series solutions method is mainly used to find power series solutions of differential equations whose solutions can not be written in terms of familiar functions such as polynomials, exponential or trigonometric functions. This means that in general you will not be able to perform the last few steps of what we just did (less worries!), all we can try to do is to come up with a general expression for the coefficients of the power series solutions.
As another introductory example, let's find the solution to the initial value problem
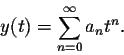
Start by plugging this "guess" into the differential equation.
Recall from the previous section that

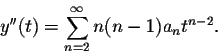
Plugging this information into the differential equation we obtain:

Our next goal is to simplify this expression such that only one summation sign "![]() " remains. The obstacle we encounter is that the powers of the three sums are different, tn-2 for the first sum tn-1 for the second sum and tn for the third. We make them the same by shifting the index of the first two sums to obtain
" remains. The obstacle we encounter is that the powers of the three sums are different, tn-2 for the first sum tn-1 for the second sum and tn for the third. We make them the same by shifting the index of the first two sums to obtain
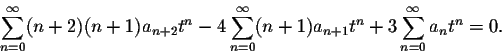
Now we can combine the sums as follows:

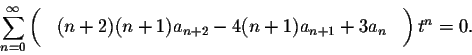
Since the power series on the left is identically equal to zero, all of its coefficients are equal to zero:
Solving these equations for the "highest index" n+2, we can rewrite
as

Recall that y(0)=a0 and y'(0)=a1, so our initial conditions imply that a0=1 and a1=2.
Reading off the recurrence relations we can compute the next coefficients:
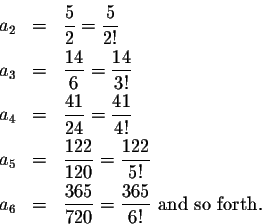
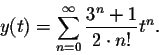

 S.O.S MATHematics home page
S.O.S MATHematics home page

1998-07-02