Series Solutions: Airy's Equation

The general form of a homogeneous second order linear differential equation looks as follows:

y''+p(t) y'+q(t) y=0.

The series solutions method is used primarily, when the coefficients p(t) or q(t) are non-constant.

One of the easiest examples of such a case is Airy's Equation

y''-t y=0,

which is used in physics to model the defraction of light.

We want to find power series solutions for this second-order linear differential equation.

The generic form of a power series is

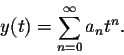
$\begin{displaymath}y(t)=\sum_{n=0}^\infty a_n t^n.\end{displaymath}$

We have to determine the right choice for the coefficients (a_n).

As in other techniques for solving differential equations, once we have a "guess" for the solutions, we plug it into the differential equation. Recall that

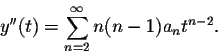
$\begin{displaymath}y''(t)=\sum_{n=2}^\infty n(n-1) a_n t^{n-2}.\end{displaymath}$

Plugging this information into the differential equation we obtain:

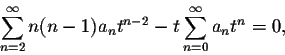
$\begin{displaymath}\sum_{n=2}^\infty n(n-1) a_n t^{n-2}-t\sum_{n=0}^\infty a_n t^n=0, \end{displaymath}$

or equivalently

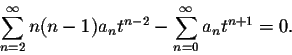
$\begin{displaymath}\sum_{n=2}^\infty n(n-1) a_n t^{n-2}-\sum_{n=0}^\infty a_n t^{n+1}=0. \end{displaymath}$

Our next goal is to simplify this expression such that (basically) only one summation sign " $\sum$ " remains. The obstacle we encounter is that the powers of both sums are different, t^n-2 for the first sum and tⁿ⁺¹ for the second sum. We make them the same by shifting the index of the first sum up by 2 units and the index of the second sum down by one unit to obtain

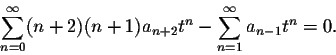
$\begin{displaymath}\sum_{n=0}^\infty (n+2)(n+1) a_{n+2} t^{n}-\sum_{n=1}^\infty a_{n-1} t^{n}=0.\end{displaymath}$

Now we run into the next problem: the second sum starts at n=1, while the first sum has one more term and starts at n=0. We split off the 0th term of the first sum:

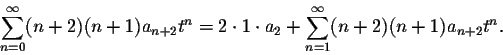
$\begin{displaymath}\sum_{n=0}^\infty (n+2)(n+1) a_{n+2} t^{n}=2\cdot 1\cdot a_2+ \sum_{n=1}^\infty (n+2)(n+1) a_{n+2} t^{n}.\end{displaymath}$

Now we can combine the two sums as follows:

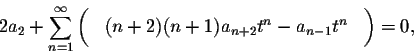
$\begin{displaymath}2 a_2 +\sum_{n=1}^\infty \left( \phantom{\int}(n+2)(n+1) a_{n+2} t^{n}- a_{n-1} t^n\phantom{\int}\right)=0,\end{displaymath}$

and factor out tⁿ:

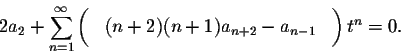
$\begin{displaymath}2 a_2+\sum_{n=1}^\infty \left( \phantom{\int}(n+2)(n+1) a_{n+2} - a_{n-1} \phantom{\int}\right)t^n=0.\end{displaymath}$

The power series on the left is identically equal to zero, consequently all of its coefficients are equal to 0:

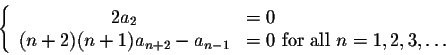
$\begin{displaymath}\left\{\begin{array}{cl}2a_2&=0\\ (n+2)(n+1) a_{n+2} - a_{n-1} &=0 \mbox{ for all } n=1,2,3,\ldots\end{array}\right.\end{displaymath}$

We can slightly rewrite as

$\begin{displaymath}\left\{\begin{array}{ll}a_2&=0\\ a_{n+2}& =\displaystyle{\fra... ...{(n+1)(n+2)}} \mbox{ for all } n=1,2,3,\ldots\end{array}\right.\end{displaymath}$

These equations are known as the "recurrence relations" of the differential equations. The recurrence relations permit us to compute all coefficients in terms of a₀ and a₁.

We already know from the 0th recurrence relation that a₂=0. Let's compute a₃ by reading off the recurrence relation for n=1:

$\begin{displaymath}a_3=\frac{a_0}{2\cdot 3}.\end{displaymath}$

Let us continue:

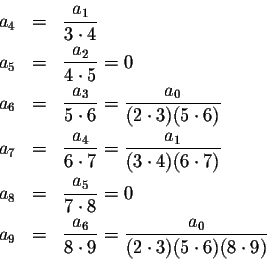
$\begin{eqnarray*}a_4&=&\frac{a_1}{3\cdot 4}\\ a_5&=&\frac{a_2}{4\cdot 5}=0\\ a... ...&\frac{a_6}{8\cdot 9}=\frac{a_0}{(2\cdot 3)(5\cdot 6)(8\cdot 9)} \end{eqnarray*}$

The hardest part, as usual, is to recognize the patterns evolving; in this case we have to consider three cases:

1. All the terms $a_2,a_5,a_8,\ldots$ are equal to zero. We can write this in compact form as

$\begin{displaymath}a_{3k+2}=0\mbox{ for all }k=0,1,2,3,\ldots\end{displaymath}$

2. All the terms $a_3,a_6,a_9,\ldots$ are multiples of a₀. We can be more precise:

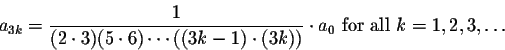
$\begin{displaymath}a_{3k}=\frac{1}{(2\cdot 3)(5\cdot 6)\cdots((3k-1)\cdot (3k))}\cdot a_0 \mbox{ for all }k=1,2,3,\ldots\end{displaymath}$

(Plug in k=1,2,3,4 to check that this works!)

3. All the terms $a_4,a_7,a_{10},\ldots$ are multiples of a₁. We can be more precise:

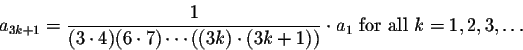
$\begin{displaymath}a_{3k+1}=\frac{1}{(3\cdot 4)(6\cdot 7)\cdots((3k)\cdot (3k+1))}\cdot a_1 \mbox{ for all }k=1,2,3,\ldots\end{displaymath}$

(Plug in k=1,2,3,4 to check that this works!)

Thus the general form of the solutions to Airy's Equation is given by

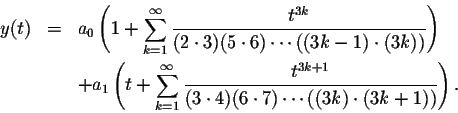
$\begin{eqnarray*}y(t)&=&a_0\left(1+\sum_{k=1}^\infty \frac{t^{3k}}{(2\cdot 3)(5\... ...{t^{3k+1}}{(3\cdot 4)(6\cdot 7)\cdots((3k)\cdot (3k+1))}\right). \end{eqnarray*}$

Note that, as always, y(0)=a₀ and y'(0)=a₁. Thus it is trivial to determine a₀ and a₁ when you want to solve an initial value problem.

In particular

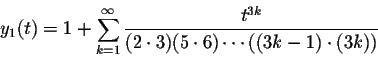
$\begin{displaymath}y_1(t)= 1+\sum_{k=1}^\infty \frac{t^{3k}}{(2\cdot 3)(5\cdot 6)\cdots((3k-1)\cdot (3k))}\end{displaymath}$

and

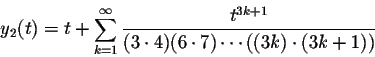
$\begin{displaymath}y_2(t)=t+\sum_{k=1}^\infty\frac{t^{3k+1}}{(3\cdot 4)(6\cdot 7)\cdots((3k)\cdot (3k+1))}\end{displaymath}$

form a fundamental system of solutions for Airy's Differential Equation.

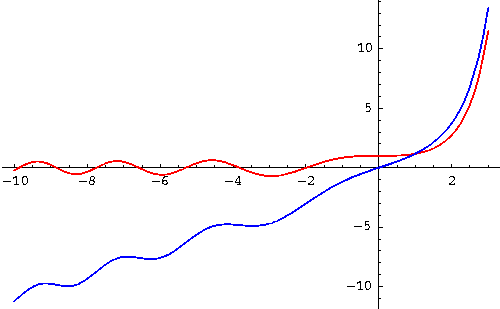
Below you see a picture of these two solutions. Note that for negative t, the solutions behave somewhat like the oscillating solutions of y''+y=0, while for positive t, they behave somewhat like the exponential solutions of the differential equation y''-y=0.

In the next section we will investigate what one can say about the radius of convergence of power series solutions.

[Back] [Next] [Algebra] [Trigonometry] [Complex Variables] [Calculus] [Differential Equations] [Matrix Algebra]

S.O.S. MATHematics home page

1998-07-03