Real Eigenvalues: Example1

Example: Consider the harmonic oscillator with spring constant 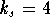, damping constant 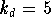, and the mass m=1.

(1)

Write down the second order equation governing this physical system. Use the letter y for the spring's displacement from its rest position.

(2)

Convert this equation into a linear system of first order differential equations.

(3)

Solve the system.

(4)

Find the particular solution which satisfies the initial conditions

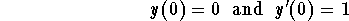
(5)

Discuss the long-term behavior of the system. Is this conclusion probable?

Solution:

Next Example:

[Differential Equations] [First Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA