Real Eigenvalues
Real Eigenvalues
Consider the linear homogeneous system
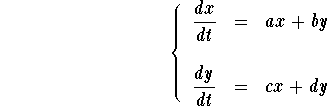
In order to find the eigenvalues, consider the characteristic polynomial
.
In this section we will consider the case of the quadratic equation
above when it has
two distinct real roots (that is, if
).
The roots (eigenvalues) are
,
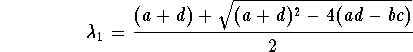and
.
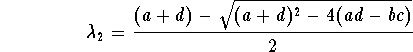Here we know that the differential system has two linearly independent straight-line solutions
,
where 
(respectively
)
is an eigenvector associated to the eigenvalue
(respectively 
).
We also know that the general solution (which describes all of the solutions) to the system has the form
.
Keep in mind that and are two constant vectors.
Let us discuss the behavior of the solutions when 
(meaning the future) and when 
(meaning the past). Since the eigenvalues are distinct, one is bigger than the other one. Assume that we have
.
It is easy to see that we have
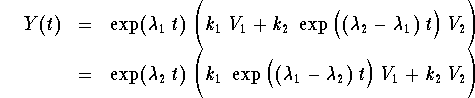
Behavior when
In this case we will consider the equation
.
Since
,
(because 
) then it is clear that when , we have
.
Behavior when
In this case we will consider the equation
Since
(because 
) then it is clear that when , we have
Remark:Since the two eigenvalues are real numbers, we have three cases to consider depending on their signs:
.
In this case we have
,
meaning that the solutions emanate from the origin (if you go to the past, you will die at the origin). When , Y(t) explodes.
|
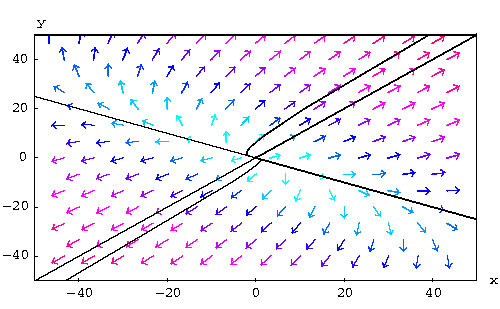
In this case the origin plays the role of a source. Clearly, the origin is the only equilibrium point.
.
In this case we have
,
meaning that in the future the solutions die at the origin. When , Y(t) explodes.
|
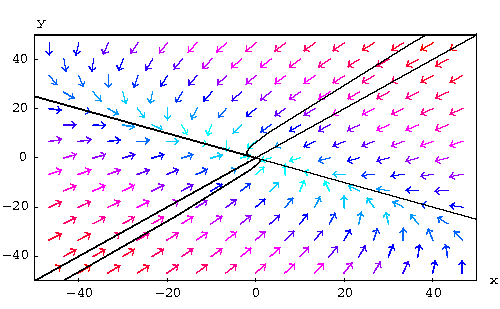
In this case, the origin plays the role of a sink. Clearly, the origin is the only equilibrium point.
.
In this case, the origin behaves like a saddle.
|
Remark: It is clear from the above discussions that one may decide about the signs of the eigenvalues just by looking at some solutions on the phase plane (depending whether we have a saddle, a sink or a source).
Example: Consider the three phase planes and decide about the sign-distribution of the associated eigenvalues.
| Phase Plane I |
|---|
|
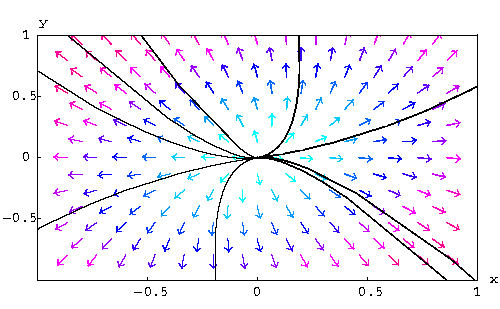
| Phase Plane II |
|
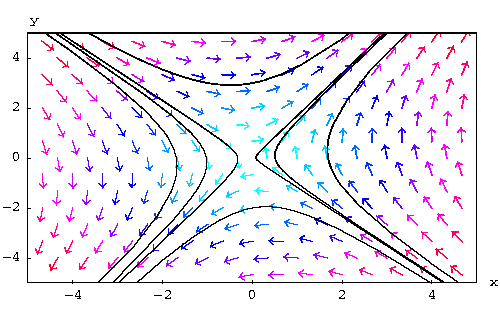
| Phase Plane III |
|
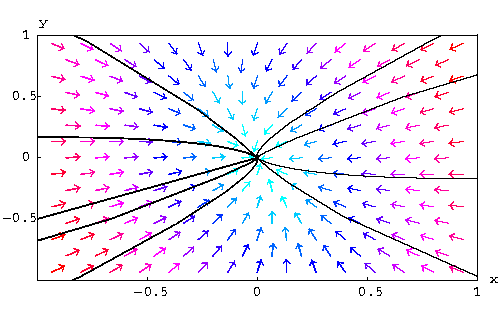
Answer:
Example: Consider the harmonic oscillator equation
.
Discuss the behavior of the spring-mass.
Answer: First, translate this equation to the system
,
where
The characteristic polynomial of this system is
.
The eigenvalues are
.
It is clear that both of them are negative. Hence, the origin is a sink. Meaning that, regardless of the initial condition, the mass will always tend to its equilibrium, or rest, position.
Note that if V is an eigenvector associated to the biggest eigenvalue 
, then all the solutions tend to the origin tangent to that vector V. In this case we have
.
|
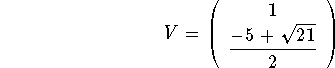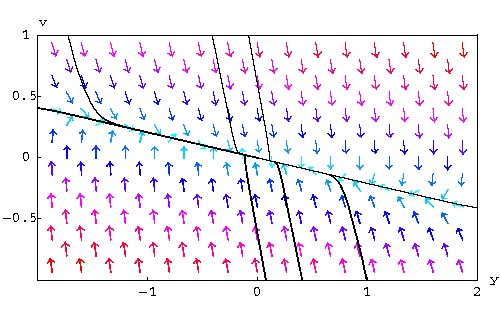
Remark: The case when one of the two eigenvalues is zero will be discussed in another section separately.
S.O.S MATHematics home page 