 SYSTEMS OF EQUATIONS in THREE VARIABLES
SYSTEMS OF EQUATIONS in THREE VARIABLES SYSTEMS OF EQUATIONS in THREE VARIABLES
SYSTEMS OF EQUATIONS in THREE VARIABLES
It is often desirable or even necessary to use more than one variable to
model a situation in a field such as business, science, psychology,
engineering, education, and sociology, to name a few. When this is the case,
we write and solve a system of equations in order to answer questions about
the situation.
If a system of linear equations has at least one solution, it is
consistent. If the system has no solutions, it is inconsistent. If
the system has an infinity number of solutions, it is dependent.
Otherwise it is independent.
A linear equation in three variables is an equation equivalent to the
equation
![]()
where
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are real numbers and
are real numbers and
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are not all
are not all
![]() .
.
Example 1:
John inherited $25,000 and invested part of it in a money market account,
part in municipal bonds, and part in a mutual fund. After one year, he
received a total of $1,620 in simple interest from the three investments.
The money market paid 6% annually, the bonds paid 7% annually, and the
mutually fund paid 8% annually. There was $6,000 more invested in the
bonds than the mutual funds. Find the amount John invested in each
category.
There are three unknowns:
1 : The amount of money invested in the money market account.
2 : The amount of money invested in municipal bonds.
3 : The amount of money invested in a mutual fund.
Let's rewrite the paragraph that asks the question we are to answer.
[The amount of money invested in the money market account +
[The amount of money invested in municipal bonds ] +
[The amount of money invested in a mutual fund ]
![]()
The 6% interest on [ The amount of money invested in the money market
account ]+ the 7% interest on [ The amount of money invested in
municipal bonds ] + the 8% interest on [ The amount of money invested
in a mutual fund ] ![]()
[The amount of money invested in municipal bonds ] -
[ The amount of money invested in a mutual fund ] =
![]() .
.
It is going to get boring if we keep repeating the phrases
1 : The amount of money invested in the money market account.
2 : The amount of money invested in municipal bonds.
3 : The amount of money invested in a mutual fund.
Let's create a shortcut by letting symbols represent these phrases. Let
x = The amount of money invested in the money market account.
y = The amount of money invested in municipal bonds.
z = The amount of money invested in a mutual fund.
in the three sentences, and then rewrite them.
The sentence [ The amount of money invested in the money market account ]
![]() [ The amount of money invested in municipal bonds ]
[ The amount of money invested in municipal bonds ]
![]() [ The amount of
money invested in a mutual fund ]
[ The amount of
money invested in a mutual fund ]
![]() can now be written as
can now be written as
![]()
The sentence The
![]() interest on [ The amount of money invested in the
money market account ]
interest on [ The amount of money invested in the
money market account ]
![]() the
the
![]() interest on [ The amount of money
invested in municipal bonds ]
interest on [ The amount of money
invested in municipal bonds ]
![]() the
the
![]() interest on [ The amount of
money invested in a mutual fund ]
interest on [ The amount of
money invested in a mutual fund ]
![]() can now be written as
can now be written as
![]()
The sentence [ The amount of money invested in municipal bonds ]
![]() [ The
amount of money invested in a mutual fund ]
[ The
amount of money invested in a mutual fund ]
![]()
![]() can now be written
as
can now be written
as
![]()
We have converted the problem from one described by words to one that is
described by three equations.
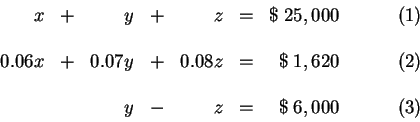
We are going to show you how to solve this system of equations three
different ways:
1) Substitution,
2) Elimination,
3) Matrices.
SUBSTITUTION:
The process of substitution involves several steps:
Step 1: Solve for one of the variables in one of the equations. It
makes no difference which equation and which variable you choose. Let's solve
for
![]() in equation (3) because the equation only has two variables.
in equation (3) because the equation only has two variables.
![]()
![]()
Step 2: Substitute this value for
![]() in equations (1) and (2). This
will change equations (1) and (2) to equations in the two variables
in equations (1) and (2). This
will change equations (1) and (2) to equations in the two variables
![]() and
and
![]() . Call the changed equations (4) and (5).
. Call the changed equations (4) and (5).
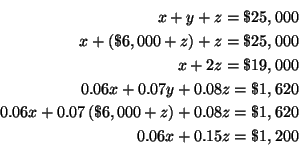
or
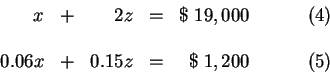
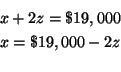
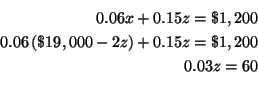
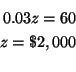
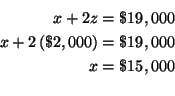
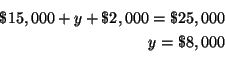
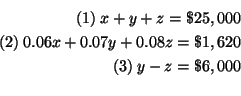
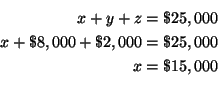
![$ \left[
\begin{array}{rrrrrrr}
1 & & 1 & & 1 & \vert & \$25,000 \\
& & & & ...
...
& & & & & \vert & \\
0 & & 1 & & 1 & \vert & \$2,000
\end{array}
\right]$](img53.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 1 & & 1 & \vert & \$25,000 \\
& & & & ...
...
& & & & & \vert & \\
0 & & 1 & & 1 & \vert & \$2,000
\end{array}
\right]$](img53.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 0 & & 0 & \vert & a \\
& & & & & \vert...
... b \\
& & & & & \vert & \\
0 & & 0 & & 1 & \vert & c
\end{array}
\right] $](img54.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 1 & & 1 & \vert & \$25,000 \\
& & & & ...
...
& & & & & \vert & \\
0 & & 1 & & 1 & \vert & \$2,000
\end{array}
\right] $](img59.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 1 & & 1 & \vert & \$25,000 \\
& & & & ...
...
& & & & & \vert & \\
0 & & 1 & & 1 & \vert & \$2,000
\end{array}
\right]$](img62.gif)
![\begin{eqnarray*}
-\left[ Row\ 2\right] +\left[ Row\ 1\right] =\left[ New\ Row\...
...\ 2\right] +\left[ Row\ 3\right] =\left[ New\ Row\ 3\right] \\
\end{eqnarray*}](img64.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 0 & & -1 & \vert & \$13,000 \\
& & & &...
...& & & & & \vert & \\
0 & & 0 & & -1 & \vert & -\$2,000
\end{array}
\right] $](img65.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 0 & & -1 & \vert & \$13,000 \\
& & & &...
...
& & & & & \vert & \\
0 & & 0 & & 1 & \vert & \$2,000
\end{array}
\right] $](img67.gif)
![\begin{eqnarray*}
1\left[ Row\ 3\right] +\left[ Row\ 1\right] =\left[ New\ Row\...
...w\ 3\right] +\left[ Row\ 2\right] =\left[ New\ Row\ 2\right]\\
\end{eqnarray*}](img68.gif)
![$ \left[
\begin{array}{rrrrrrr}
1 & & 0 & & 0 & \vert & \$15,000 \\
& & & & ...
...
& & & & & \vert & \\
0 & & 0 & & 1 & \vert & \$2,000
\end{array}
\right] $](img69.gif)
If you would like to work a similar example, click on Example.
If you would like to test yourself by working some problem similar to this example, click on
Problem.

