SYSTEMS OF EQUATIONS in THREE VARIABLES

It is often desirable or even necessary to use more than one variable to model situations in many fields. We write and solve a system of equations in order to answer questions about the situation.

If a system of linear equations has at least one solution, it is consistent. If the system has no solutions, it is inconsistent. If the system has an infinity number of solutions, it is dependent. Otherwise it is independent.

A linear equation in three variables is an equation equivalent to the equation

$$\begin{eqnarray*}&& \\ Ax+By+Cz+D &=&0 \\ && \end{eqnarray*}$$

where A, B, C, and D are real numbers and A, B, C, and D are not all 0. This is the equation of a plane.

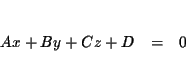
Work the following problems. Click on Solution, if you want to review the solutions.

Problem 3.1a:

A total of $50,000 is invested in three funds paying 6%, 8%, and 10% simple interest. The yearly interest is $3,700. Twice as much money is invested at 6% as invested at 10%. How much is invested in each of the funds.

Solution

Problem 3.1b:

The standard equation of a circle is x²+y²+Ax+By+C=0. Find the equation of the circle that passes through the points $\left( 1,1\right)$, $% \left( 2,-4\right)$, and $\left( 5,5\right) .$

Solution

Problem 3.1c:

Your company has three acid solutions on hand: 30%, 40%, and 80% acid. It can mix all three to come up with a 100-gallons of a 39% acid solution. If it interchanges the amount of 30% solution with the amount of the 80% solution in the first mix, it can create a 100-gallon solution that is 59% acid. How much of the 30%, 40%, and 80% solutions did the company mix to create a 100-gallons of a 39% acid solution?

Solution

Problem 3.1d:

Five hundred tickets were sold for a certain music concert. The tickets for the adults sold for $7.50, the tickets for the children sold for $4.00, and tickets for senior citizen sold for $3.50. The revenue for the Monday performance was $3,025. Twice as many adult tickets were sold as children tickets. How many of each ticket was sold?

Solution

Problem 3.1e:

Solve the following system of equations for x, y and z:

$$\begin{eqnarray*}&& \\ 7x+5y-3z &=&16 \\ && \\ 3x-5y+2z &=&-8 \\ && \\ 5x+3y-7z &=&0 \\ && \end{eqnarray*}$$

Solution

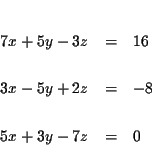
Problem 3.1f:

Solve the following system of equations for x, y and z:

$$\begin{eqnarray*}&& \\ \frac{7}{2}x+\frac{2}{5}y-3z &=&-217 \\ && \\ \frac... ...rac{8}{21}z &=&6 \\ && \\ 5x+3y-\frac{7}{4}z &=&-12 \\ && \end{eqnarray*}$$

Solution

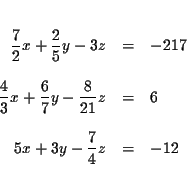
If you would like to return to the beginning of the two by two system of equations, click on start.

If you would like to review three-variable systems example, click on three.

[Two-Variable Systems] [Three-Variable Systems] [Algebra] [Geometry] [Trigonometry ]

S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA