SYSTEMS OF EQUATIONS in THREE VARIABLES

It is often desirable or even necessary to use more than one variable to model a situation in many fields. When this is the case, we write and solve a system of equations in order to answer questions about the situation.

If a system of linear equations has at least one solution, it is consistent. If the system has no solutions, it is inconsistent. If the system has an infinity number of solutions, it is dependent. Otherwise it is independent.

A linear equation in three variables describes a plane and is an equation equivalent to the equation

$$\begin{eqnarray*}&& \\ Ax+By+Cz+D &=&0 \\ && \end{eqnarray*}$$

where A, B, C, and D are real numbers and A, B, C, and D are not all 0.

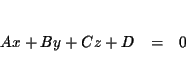
Problem 3.1b:

The standard equation of a circle is x²+y²+Ax+By+C=0. Find the equation of the circle that passes through the points $\left( 1,1\right)$, $% \left( 2,-4\right)$, and $\left( 5,5\right)$

Answer:

x²+y²-13x+y+10=0

Solution:

Let's create three equations from the given points.

$$\rightarrow \left( 1\right) ^{2}+\left( 1\right) ^{2}+A\left( 1\right) +B\left( 1\right) +C=0$$ (1,11)

A+B+C = -2 (1)

$$\rightarrow \left( 2\right) ^{2}+\left( -4\right) ^{2}+A\left( 2\right) +B\left( -4\right) +C=0$$ (2,-4)

2A-4B+C = -20 (2)

$$\rightarrow \left( 5\right) ^{2}+\left( 5\right) ^{2}+A\left( 5\right) +B\left( 5\right) +C=0$$ (5,5)

5A+5B+C = -50 (3)

We are going to show you how to solve this system of equations three different ways:

1)        Substitution, 2)        Elimination 3)        Matrices

SUBSTITUTION:

The process of substitution involves several steps:

Step 1:        Solve for one of the variables in one of the equations. It makes no difference which equation and which variable you choose. Let's solve for C in equation (1).

$$\begin{eqnarray*}&& \\ A+B+C &=&-2 \\ && \\ C &=&-A-B-2 \\ && \\ && \end{eqnarray*}$$

Step 2:        Substitute this value for C in equations (2) and (3). This will change equations (2) and (3) to equations in the two variables A and B. Call the changed equations (4) and (5), respectively.

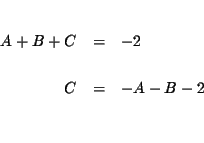
(2) : 2A-4B+C=-20

$$2A-4B+\left( -A-B-2\right)$$ = -20

A-5B = -18 (4)

(3) : 5A+5B+C=-50

$$5A+5B+\left( -A-B-2\right)$$ = -50

4A+4B = -48

A+B = -12 (5)

Step 3:        Solve for A in equation (4).

$$\begin{eqnarray*}&& \\ (4) &:&A-5B=-18 \\ && \\ A &=&5B-18 \\ && \\ && \\ && \\ && \end{eqnarray*}$$

Step 4:        Substitute this value of A in equation (5). This will give you an equation in one variable.

$$\begin{eqnarray*}&& \\ (5) &:&A+B=-12 \\ && \\ \left( 5B-18\right) +B &=&-12 \\ && \\ && \\ && \end{eqnarray*}$$

Step 5:         Solve for B.

$$\begin{eqnarray*}&& \\ \left( 5B-18\right) +B &=&-12 \\ && \\ 6B &=&6 \\ && \\ B &=&1 \\ && \\ && \end{eqnarray*}$$

Step 6:        Substitute this value of B in equation (4) and solve for A.

$$\begin{eqnarray*}&& \\ (4) &:&A-5B=-18 \\ && \\ A-5\left( 1\right) &=&-18 \\ && \\ A &=&-13 \\ && \\ && \end{eqnarray*}$$

Step 7:        Substitute -13 for A and 1 for B in equation (1) and solve for C.

$$\begin{eqnarray*}&& \\ (1) &:&A+B+C=-2 \\ && \\ \left( -13\right) +\left( 1\right) +C &=&-2 \\ && \\ C &=&10 \\ && \\ && \end{eqnarray*}$$

The solution: The equation of the circle that contains the points $\left( 1,1\right)$, $\left( 2,-4\right)$, and $\left( 5,5\right)$ is

$$\begin{eqnarray*}&& \\ x^{2}+y^{2}-13x+y+10 &=&0 \\ && \\ && \end{eqnarray*}$$

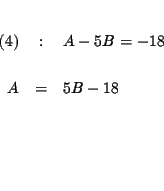
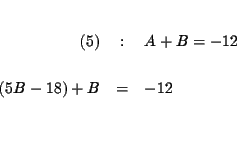
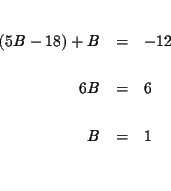
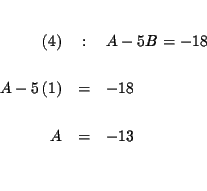
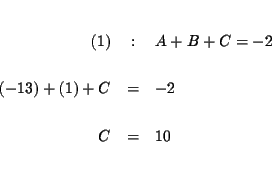
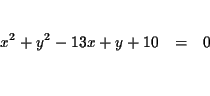
Step 8:        Check the solutions:

$$\begin{eqnarray*}&& \\ (1,1) &:&(1)^{2}+\left( 1\right) ^{2}-13\left( 1\right)... ... 5\right) +10=0\rightarrow Yes \\ && \\ && \\ && \\ && \end{eqnarray*}$$

ELIMINATION:

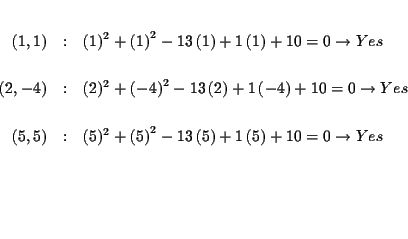
The process of elimination involves several steps: First you reduce three equations to two equations with two variables, and then to one equation with one variable.

Step 1:        Decide which variable you will eliminate. It makes no difference which one you choose. Let us eliminate C first.

$$\begin{eqnarray*}&& \\ && \begin{array}{lllllllll} (1) & : & A & + & B & + &... ...: & 5A & + & 5B & + & C & = & -50 \end{array} \\ && \\ && \end{eqnarray*}$$

Step 2:        Add -1 times equations (1) to equation (2) to form equation (4), then add -1 times equations (2) to equation (3) to form equation (5). Equations (4) and (5) will contain the variables A and B.

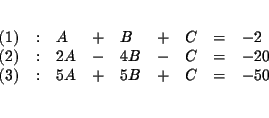
$$\begin{eqnarray*}&& \\ -1\left[ Equation\ 1\right] +\left[ Equation\ 2\right] ... ...right] +\left[ Equation\ 3\right] &=&\left[ Equation\ 5\right] \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{lllllllll} (1) & : & -A & - & B & - ... ...& = & -50 \\ (5) & : & 3A & + & 9B & & & = & -30 \end{array} \end{eqnarray*}$$

Step 3:        We now have two equations with two variables. Let's simplify these Equation(5).

$$\begin{eqnarray*}(4) &:&A-5B=-18 \\ && \\ && \\ (5) &:&3A+9B=-30 \\ && \\ A+3B &=&-10 \\ && \\ && \end{eqnarray*}$$

Step 4:        Add the -1 times equation (4) to equation (5) to create equation (6) with just one variable.

$\begin{array}{lllllll} (4) & : & -A & + & 5B & = & 18 \\ (5) & : & A & + & 3B & = & -10 \\ (6): & & & & 8B= & & 8 \end{array}$

Step 5:        Solve for A in equation (6).

$$\begin{eqnarray*}&& \\ 8B &=&8 \\ && \\ B &=&1 \\ && \\ && \end{eqnarray*}$$

Step 6:        Substitute 1 for B in equation (4) and solve for B.

$$\begin{eqnarray*}&& \\ (4) &:&A-5B=-18 \\ && \\ A-5\left( 1\right) &=&-18 \\ && \\ A &=&-13 \\ && \\ && \end{eqnarray*}$$

Step 7:        Substitute -13 for A and 1 for B in equation (1) and solve for C.

$$\begin{eqnarray*}&& \\ (1) &:&A+B+C=-2 \\ && \\ \left( -13\right) +\left( 1\right) +C &=&-2 \\ && \\ C &=&100 \\ && \\ && \end{eqnarray*}$$

The equation of the circle is $x^{2}+y^{2}-13x+y+10=0\medskip\medskip$ Check your answers as before.

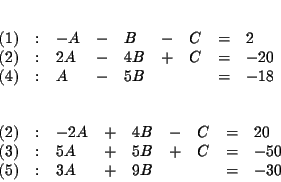
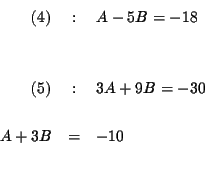
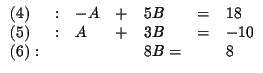
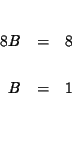
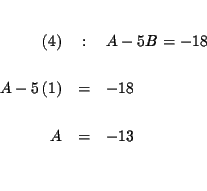
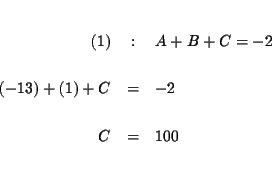
MATRICES:

The process of using matrices is essentially a shortcut of the process of elimination. Each row of the matrix represents an equation and each column represents coefficients of one of the variables.

Step 1: Create a three-row by four-column matrix using coefficients and the constant of each equation.

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ... \\ 5 & & 5 & & 1 & \vert & -50 \end{array} \right] \\ && \end{eqnarray*}$$

The vertical lines in the matrix stands for the equal signs between both sides of each equation. The first column contains the coefficients of A, the second column contains the coefficients of B, the third column contains the coefficients of C, and the last column contains the constants to the right of the equal signs.

We want to convert the original matrix

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ... \\ 5 & & 5 & & 1 & \vert & -50 \end{array} \right] \\ && \end{eqnarray*}$$

to the equivalent matrix.

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ... & & & & \\ 0 & & 0 & & 1 & & c \end{array} \right] \\ && \end{eqnarray*}$$

Then you can read the matrix as A=a, B=b, and C=c..

Step 2:        We work with column 1 first. We want a 1 in Cell 11 [Row 1-Col 1]. There is nothing to do because 1 already exits in the Cell 22. Now we want zeros in Cells 21 and 31. To achieve this, Add -2 times Row 1 to Row 2 to form a new Row 2, and add -5 times Row 1 to Row 3 to form a new Row 3.

$$\begin{eqnarray*}&& \\ -2\left[ Row\ 1\right] +\left[ Row\ 2\right] &=&\left[ ... ...ow\ 1\right] +\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right] \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ...\\ 0 & & 0 & & -4 & \vert & -40 \end{array} \right] \\ && \end{eqnarray*}$$

Step 4:        Let's now manipulate the matrix so that there is a 1 in Cell 22. We do this by multiplying Row 2 by $-\dfrac{1}{6}.$

$$\begin{eqnarray*}&& \\ -\dfrac{1}{6}\left[ Row\ 2\right] &=&\left[ New\ Row\ 2\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ...\\ 0 & & 0 & & -4 & \vert & -40 \end{array} \right] \\ && \end{eqnarray*}$$

Step 5:        Let's now manipulate the matrix so that there are zeros in Cell 12 and Cell 32. We do this by adding -1 times Row 2 to Row 1 to form a new Row 1

$$\begin{eqnarray*}&& \\ -1\left[ Row\ 2\right] +\left[ Row\ 1\right] &=&\left[ New\ Row\ 1\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ...\\ 0 & & 0 & & -4 & \vert & -40 \end{array} \right] \\ && \end{eqnarray*}$$

Step 6:        Let's now manipulate the matrix so that there is a 1 in Cell 33. We do this by multiplying Row 3 by $-\dfrac{1}{4}.$

$$\begin{eqnarray*}&& \\ -\dfrac{1}{4}\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ...& \\ 0 & & 0 & & 1 & \vert & 10 \end{array} \right] \\ && \end{eqnarray*}$$

Step 7:        Let's now manipulate the matrix so that there are zeros in Cells 13 and 12.

$$\begin{eqnarray*}&& \\ -\dfrac{5}{6}\left[ Row\ 3\right] +\left[ Row\ 1\right]... ...ht] +\left[ Row\ 2\right] &=&\left[ New\ Row\ 2\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{l} \left( 1\right) \\ \\ \left( ... ...& \\ 0 & & 0 & & 1 & \vert & 10 \end{array} \right] \\ && \end{eqnarray*}$$

You can now read the answers off the matrix: A=-13, B=1, and C=10. check your answers by the method described above.

If you would like to go back to the problem page, click on Problem.

If you would like to review the solution to the next problem, click on Problem

If you would like to return to the beginning of the three by three system of equations, click on Example.

[Two--Variable Systems] [Three-Variable Systems] [Algebra] [Geometry] [Trigonometry ]

S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA