SYSTEMS OF EQUATIONS in THREE VARIABLES

It is often desirable or even necessary to use more than one variable to model a situation in many fields. When this is the case, we write and solve a system of equations in order to answer questions about the situation.

If a system of linear equations has at least one solution, it is consistent. If the system has no solutions, it is inconsistent. If the system has an infinity number of solutions, it is dependent. Otherwise it is independent.

A linear equation in three variables describes a plane and is an equation equivalent to the equation

$$\begin{eqnarray*}&& \\ Ax+By+Cz+D &=&0 \\ && \end{eqnarray*}$$

where A, B, C, and D are real numbers and A, B, C, and D are not all 0.

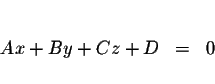
Problem 3.1d:

Five hundred tickets were sold for a certain music concert. The tickets for the adults sold for $7.50, the tickets for the children sold for $4.00, and tickets for senior citizen sold for $3.50. The revenue for the Monday performance was $3,025. Twice as many adult tickets were sold as children tickets. How many of each ticket was sold?

Answer:         300 adult tickets, 150 children tickets, and 50 senior citizen tickets.

Solution:

There are three unknowns:

$$\begin{eqnarray*}&& \\ 1 &:&\text{ The number of adult tickets sold} \\ 2 &:... ... 3 &:&\text{ The amount of senior citizen tickets sold} \\ && \end{eqnarray*}$$

Let's rewrite the paragraph that asks the question we are to answer.

The first sentence can be rewritten as [ The number of adult tickets sold ] + [ The amount of children tickets sold ] + [ The amount of senior citizen tickets sold ] $=500.\bigskip$ The second sentence can be rewritten $\$7.50$ times [ The number of adult tickets sold ] $+\ \$4.00$ times [ The amount of children tickets sold ] + $\$3.50$ times [ The amount of senior citizen tickets sold ] $% =\$3,025.\bigskip$ The third sentence can be rewritten [ The number of adult tickets sold ] = twice [ The amount of children tickets sold ].

It is going to get boring if we keep repeating the phrases

$$\begin{eqnarray*}&& \\ 1 &:&\text{ The number of adult tickets sold} \\ 2 &:... ... 3 &:&\text{ The amount of senior citizen tickets sold} \\ && \end{eqnarray*}$$

Let's create a shortcut by letting symbols represent these phrases. Let

$$\begin{eqnarray*}&& \\ x &=&\text{ The number of adult tickets sold} \\ y &=... ... z &=&\text{ The amount of senior citizen tickets sold} \\ && \end{eqnarray*}$$

in the three sentences, and then rewrite them.

The first sentence [ The number of adult tickets sold ] + [ The amount of children tickets sold ] + [ The amount of senior citizen tickets sold ] =500 can now be written in the algebraic form

$$\begin{eqnarray*}&& \\ x+y+z &=&500 \\ && \\ && \end{eqnarray*}$$

The second sentence $\$7.50$ times [ The number of adult tickets sold ] $% +\$4.00$ times [ The amount of children tickets sold ] + $\$3.50$ times [ The amount of senior citizen tickets sold ] $=\$3,025$ can now be written in the algebraic form

$$\begin{eqnarray*}&& \\ 7.50x+4.00y+3.50z &=&3,025 \\ && \\ && \end{eqnarray*}$$

The third sentence [ The number of adult tickets sold ] = twice [ The amount of children tickets sold ] can now be written in the algebraic form

$$\begin{eqnarray*}&& \\ x &=&2y \\ && \\ && \end{eqnarray*}$$

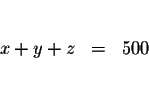
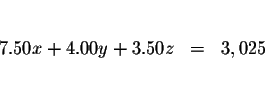
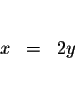
We have converted the problem from one described by words to one that is described by three equations.

x+y+z = 500 (1)

7.50x+4.00y+3.50z = 3,025 (2)

x-2y = 0 (3)

We are going to show you how to solve this system of equations three different ways:

1)        Substitution, 2)        Elimination 3)        Matrices

SUBSTITUTION:

The process of substitution involves several steps:

Step 1:        Solve for one of the variables in one of the equations. It makes no difference which equation and which variable you choose. Let's solve for x in equation (3).

$$\begin{eqnarray*}&& \\ x-2y &=&0 \\ && \\ x &=&2y \\ && \\ && \end{eqnarray*}$$

Step 2:        Substitute this value for x in equations (1) and (2). This will change equations (1) and (3) to equations in the two variables y and z. Call the changed equations (4) and (5), respectively.

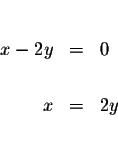
x+y+x = 500

2y+y+z = 500

3y+z = 500 (4)

7.50x+4.00y+3.50z = 3,025

$$7.50\left( 2y\right) +4.00y+3.50z$$ = 3,025

19y+3.50z = 3,025 (5)

Step 3:        Solve for z in equation (4).

$$\begin{eqnarray*}&& \\ 3y+z &=&500 \\ && \\ z &=&-3y+500 \\ && \\ && \\ && \\ && \end{eqnarray*}$$

Step 4:        Substitute this value of z in equation (5). This will give you an equation in y. Solve for y.

$$\begin{eqnarray*}&& \\ 19y+3.50z &=&3,025 \\ && \\ 19y+3.50\left( -3y+500\... ...&3,025 \\ && \\ 8.5y &=&1,275 \\ && \\ y &=&150 \\ && \end{eqnarray*}$$

Step 5:        Substitute this value of y in equation (4) and solve for z.

$$\begin{eqnarray*}&& \\ 3y+z &=&500 \\ && \\ 3\left( 150\right) +z &=&500 \\ && \\ z &=&50 \\ && \\ && \end{eqnarray*}$$

Step 7:        Substitute 150 for y and 50 for z in equation (1) and solve for x.

$$\begin{eqnarray*}&& \\ x+y+y &=&500 \\ && \\ x+150+50 &=&500 \\ && \\ x &=&300 \\ && \end{eqnarray*}$$

The solution is: $x=300,\ y=150,$ and z=50. In terms of the original problems, 300 adult tickers were sold, 150 children tickets were sold, and 50 senior citizen tickets were sold.

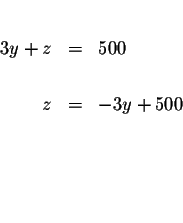
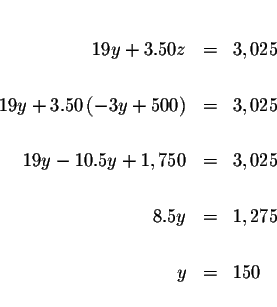
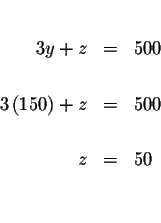
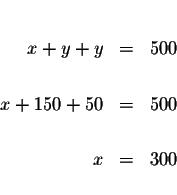
Step 8:        Check the solutions:

$$\begin{eqnarray*}&& \\ 300+150+50 &=&500\rightarrow Yes \\ && \\ 7.50\left... ...eft( 150\right) \rightarrow Yes \\ && \\ && \\ && \\ && \end{eqnarray*}$$

ELIMINATION:

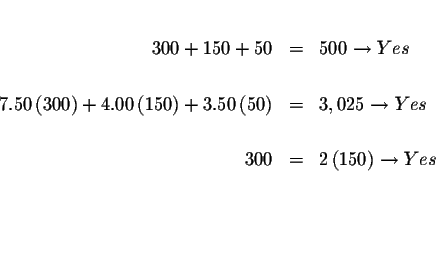
The process of elimination involves several steps: First you reduce three equations to two equations with two variables, and then to one equation with one variable.

Step 1:        Decide which variable you will eliminate. It makes no difference which one you choose. Let us eliminate x first.

$$\begin{eqnarray*}&& \\ \begin{array}{l} (1) \\ \\ (2) \\ \\ (3) \end... ...- & 2y & & & = & 0 \end{array} \end{array} & \\ && \\ && \end{eqnarray*}$$

Step 2:        Multiply both sides of equation (1) by -3.50 and then add the transformed equation (1) to equation (2) to form equation (4).

$$\begin{eqnarray*}&& \\ \begin{array}{l} (1) \\ \\ (2) \\ \\ (4) \end... ...0y & & & = & 1,275 \end{array} \end{array} & \\ && \\ && \end{eqnarray*}$$

Step :        We now have two equations with two variables.

$$\begin{eqnarray*}&& \\ (3) &:&x-2y=0 \\ && \\ (4) &:&4.00x+0.50y=1,275 \\ && \\ && \end{eqnarray*}$$

Step 4:        Multiply both sides of equation (4) by 4 and add the transformed equation (4) to equation (3) to create equation (5) with just one variable.

$\begin{array}{r} (4) \\ \\ (3) \\ \\ (5) \end{array} \ \begin{arr... ... & \\ x & - & 2y & = & 0 \\ & & & & \\ 17x & & & = & 5,100 \end{array}$

Step 5:        Solve for x in equation (5).

$$\begin{eqnarray*}&& \\ 17x &=&5,100 \\ && \\ x &=&300 \\ && \\ && \end{eqnarray*}$$

Step 6:        Substitute 300 for x in equation (3) and solve for y.

$$\begin{eqnarray*}&& \\ x-2y &=&0 \\ && \\ 300-2y &=&0 \\ && \\ y &=&150 \\ && \\ && \\ && \end{eqnarray*}$$

Step 7:        Substitute 300 for x and 150 for y in equation (1) and solve for x.

$$\begin{eqnarray*}&& \\ x+y+z &=&500 \\ && \\ 300+150+z &=&500 \\ && \\ z &=&50 \\ && \\ && \end{eqnarray*}$$

The solution is: $x=300,\ y=150,$ and z=50. In terms of the original problems, 300 adult tickers were sold, 150 children tickets were sold, and 50 senior citizen tickets were sold.

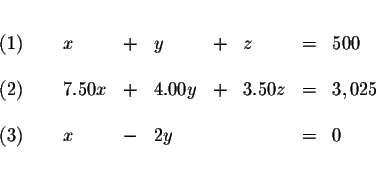
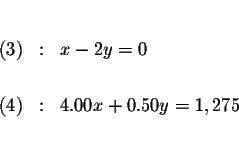
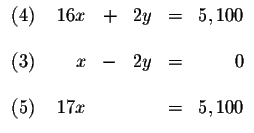
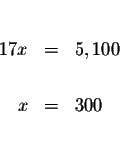
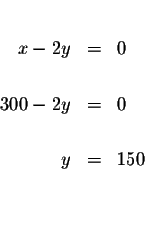
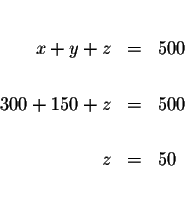
MATRICES:

The process of using matrices is essentially a shortcut of the process of elimination. Each row of the matrix represents an equation and each column represents coefficients of one of the variables.

Step 1: Create a three-row by four-column matrix using coefficients and the constant of each equation.

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ...t & \\ 1 & & -2 & & & \vert & 0 \end{array} \right] \\ && \end{eqnarray*}$$

The vertical lines in the matrix stands for the equal signs between both sides of each equation. The first column contains the coefficients of x, the second column contains the coefficients of y, the third column contains the coefficients of z, and the last column contains the constants.

We want to convert the original matrix

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ...t & \\ 1 & & -2 & & & \vert & 0 \end{array} \right] \\ && \end{eqnarray*}$$

to the following matrix.

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ... & \\ 0 & & 0 & & 1 & \vert & c \end{array} \right] \\ && \end{eqnarray*}$$

Because then you can read the matrix as x=a, y=b, and z=c..

Step 2:        We work with column 1 first. The number 1 is already in cell 11(Row1-Col 1). Add -7.50 times Row 1 to Row 2 to form a new Row 2, and add -1 times Row 1 to Row 3 to form a new Row 3..

$$\begin{eqnarray*}&& \\ -7.50\left[ Row\ 1\right] +\left[ Row\ 2\right] &=&\lef... ...ght] +\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ... 0 & & -3 & & -1 & \vert & -500 \end{array} \right] \\ && \end{eqnarray*}$$

Step 3:        We will now work with column 1. We want 1 in Cell 22, and we achieve this by multiplying Row 2 by $-\frac{1}{3.5}$ for a new Row 2.

$$\begin{eqnarray*}&& \\ -\frac{1}{3.5}\left[ Row\ 2\right] &=&\left[ New\ Row\ 2\right] \\ && \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ... 0 & & -3 & & -1 & \vert & -500 \end{array} \right] \\ && \end{eqnarray*}$$

Step 4:        Let's now manipulate the matrix so that there are zeros in Cell 12 and Cell 32. We do this by adding -1 times Row 2 to Row 1 to form a new Row 1, and adding 3 times Row 2 to Row 3 to form a new Row 3.

$$\begin{eqnarray*}&& \\ -1\left[ Row\ 2\right] +\left[ Row\ 1\right] &=&\left[ ... ...ght] +\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ...ac{17}{7} & \vert & \frac{850}{7} \end{array} \right] \\ && \end{eqnarray*}$$

Step 5:        Let's now manipulate the matrix so that there is a 1 in Cell 33. We do this by multiplying Row 3 by $\frac{7}{17}.$

$$\begin{eqnarray*}&& \\ \frac{7}{17}\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ...& \\ 0 & & 0 & & 1 & \vert & 50 \end{array} \right] \\ && \end{eqnarray*}$$

Step 6:        Let's now manipulate the matrix so that there are zeros in Cell 13 and Cell 23. We do this by adding $\frac{1}{7}$ times Row 3 to Row 1 for a new Row 1 and adding $-\frac{8}{7}$ times Row 3 to Row 2 for a new Row 2.

$$\begin{eqnarray*}&& \\ \frac{1}{7}\left[ Row\ 3\right] +\left[ Row\ 1\right] &... ...ht] +\left[ Row\ 2\right] &=&\left[ New\ Row\ 2\right] \\ && \end{eqnarray*}$$

$$\begin{eqnarray*}&& \\ && \begin{array}{r} (1) \\ \\ (2) \\ \\ (3) ... ...& \\ 0 & & 0 & & 1 & \vert & 50 \end{array} \right] \\ && \end{eqnarray*}$$

The solution is: $x=300,\ y=150,$ and z=50. In terms of the original problems, 300 adult tickers were sold, 150 children tickets were sold, and 50 senior citizen tickets were sold.

If you would like to go back to the problem page, click on Problem.

If you would like to review the solution to the next problem, click on Problem

If you would like to return to the beginning of the three by three system of equations, click on Example.

[Two--Variable Systems] [Three-Variable Systems] [Algebra] [Geometry] [Trigonometry ]

S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA