Absolute Value Inequalities

The ``forget the minus sign" definition of the absolute value is useless for our purposes. Instead, we will mostly use the geometric definition of the absolute value:

The absolute value of a number measures its distance to the origin on the real number line.

Since 5 is at 5 units distance from the origin 0, the absolute value of 5 is 5, |5|=5

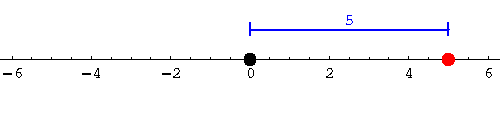
Since -5 is also at a distance of 5 units from the origin, the absolute value of -5 is 5, |-5|=5:

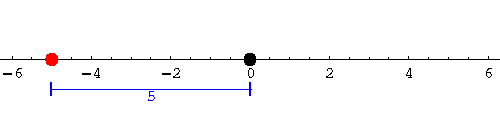
We are ready for our first inequality. Find the set of solutions for

|x|<5.

Translate into English: we are looking for those real numbers x whose distance from the origin is less than 5 units.

Obviously we are talking about the interval (-5,5):

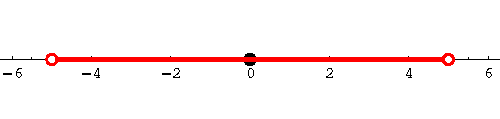
What about the solutions to $\vert x\vert\geq 2$ ?

In English: which numbers, x, are at least 2 units away from the origin? On the left side, real numbers less than or equal to -2 qualify, on the right all real numbers greater than or equal to 2:

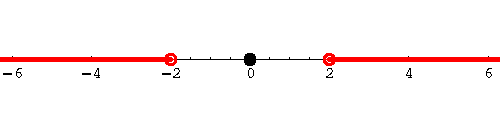
We can write this interval notation as

$\begin{displaymath}(-\infty,-2]\cup[2,\infty).\end{displaymath}$

What is the geometric meaning of |x-y|?

|x-y| is the distance between x and y on the real number line.

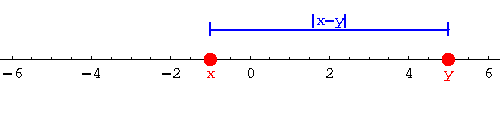
Consider the example |(-4)-3|. The distance on the real number line between the points -4 and +3 is 7, thus

|(-4)-3|=7.

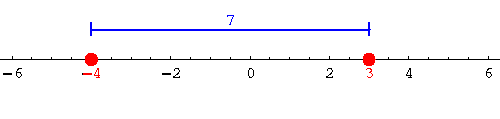
Let's find the solutions to the inequality:

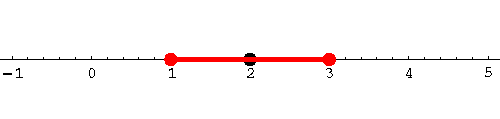
$\begin{displaymath}\vert x-2\vert\leq 1.\end{displaymath}$

In English: Which real numbers are not more than 1 unit apart from 2?

We're talking about the numbers in the interval [1,3].

What about the example

$\begin{displaymath}\vert x+1\vert\geq 3?\end{displaymath}$

Let's rewrite this as

$\begin{displaymath}\vert x-(-1)\vert\geq 3,\end{displaymath}$

which we can translate into the quest for those numbers x whose distance to -1 is at least 3.

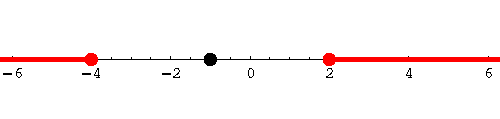
The set of solutions is

$\begin{displaymath}(-\infty,-4]\cup[2,\infty).\end{displaymath}$

With a little bit of tweaking, our method can also handle inequalities such as

|2x-5|<2.

We first divide both sides by 2. Note that absolute values interact nicely with multiplication and division:

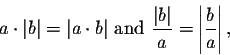
$\begin{displaymath}a\cdot \vert b\vert=\vert a\cdot b\vert \mbox{ and }\frac{\vert b\vert}{a}=\left\vert\frac{b}{a}\right\vert,\end{displaymath}$

as long as a is positive.

Thus we obtain

$\begin{displaymath}\left\vert\frac{2x-5}{2}\right\vert<\frac{2}{2};\end{displaymath}$

after simplification, we get the inequality

$\begin{displaymath}\left\vert x-\frac{5}{2}\right\vert<1,\end{displaymath}$

asking the question, which numbers are less than 1 unit apart from $\frac{5}{2}.$

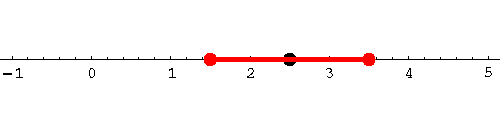
So the original inequality has as its set of solutions the interval $\left(\frac{3}{2},\frac{7}{2}\right)$ .

Consider the example

$\begin{displaymath}\vert\pi-3x\vert\geq 2.\end{displaymath}$

Let's divide by 3:

$\begin{displaymath}\left\vert\frac{\pi}{3}-x\right\vert\geq \frac{2}{3},\end{displaymath}$

which is the same as

$\begin{displaymath}\left\vert x-\frac{\pi}{3}\right\vert\geq \frac{2}{3}.\end{displaymath}$

Which numbers have distance at least $\frac{2}{3}$ from $\frac{\pi}{3}$ ? The set of solutions is given by

$\begin{displaymath}\left(-\infty,\frac{\pi}{3}-\frac{2}{3}\right]\cup\left[\frac{\pi}{3}+\frac{2}{3},+\infty\right).\end{displaymath}$

Our method fails for more contrived examples.

Let us consider the inequality

|x-3|<2x-4

It's back to basic algebra with a twist.

The standard definition for the absolute value function is given by:

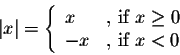
$\begin{displaymath}\vert x\vert=\left\{\begin{array}{ll} x &\mbox{, if }x\geq 0\\ -x &\mbox{, if }x<0 \end{array} \right.\end{displaymath}$

Thus we can get rid of the $\vert\mbox{ }\vert$ sign in our inequality if we know whether the expression inside, x-3, is positive or negative.

We will do exactly that!

Let's first consider only those values of x for which $x-3\geq 0$ :

Case 1: $x\geq3$

In this case we know that |x-3|=x-3, so our inequality becomes

x-3<2x-4

Solving the inequality, we obtain

x>1.

We have found some solutions to our inequality:

x is a solution if $x\geq3$ and x>1 at the same time! We're talking about numbers $x\geq3$ .

What if x-3<0?

Case 2: x<3

This time x-3<0, so |x-3|=-(x-3)=3-x, so our inequality reads as

3-x<2x-4.

Applying the standard techniques, this can be simplified to

$\begin{displaymath}x>\frac{7}{3}.\end{displaymath}$

Our inequality has some more solutions:

Under our case assumption x<3, solutions are those real numbers which satisfy $x>\frac{7}{3}$ .

We're talking about numbers in the interval

$\begin{displaymath}\left(\frac{7}{3},3\right)\end{displaymath}$

Combining the solutions we found for both cases, we conclude that the set of solutions for the inequality

|x-3|<2x-4

are the numbers in the interval

$\begin{displaymath}\left(\frac{7}{3},+\infty\right).\end{displaymath}$

1998-06-08

Absolute Value Inequalities

Exercise 1.

Answer.

Exercise 2.

Answer.

Exercise 3.

Answer.

Exercise 4.

Answer.

Exercise 5.

Answer.