Note:
If you would like an in-depth review of exponents, the rules of exponents, exponential functions and exponential equations, click on exponential function.
Solve for x in the following equation.
Example 2: 
The exponential term is already isolated.
Take the natural logarithm of both sides of the equation 
The exact answer is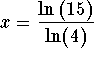 
and the
approximate answer is 
When solving the above problem, you could have used any logarithm. For example, let's solve it using the logarithm with base 8.
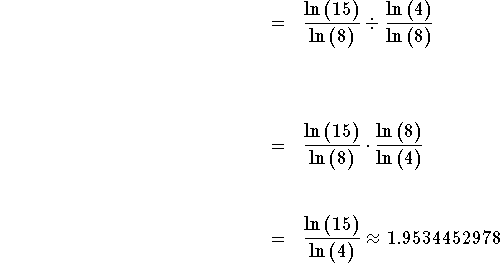
Check this answer in the original equation.
Check the solution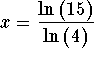 
by substituting 1.9534452978 in the original equation for x. If the left
side of the equation equals the right side of the equation after the
substitution, you have found the correct answer.
You can also check your answer by graphing 
(formed by subtracting the right side of the original equation from the left
side). Look to see where the graph crosses the x-axis; that will be the real
solution. Note that the graph crosses the x-axis at 1.9534452978. This
means that 1.9534452978 is the real solution.
If you would like to work another example, click on example.
If you would like to go to the next section, click on next.
If you would like to back to the beginning of this section, click on beginning.
If you would like to back to the last section, click on last.
If you would like to test yourself by working some problems similar to this example, click on problem.
If you would like to go back to the equation table of contents, click on contents.
