 Monotonicity and the Sign of the Derivative
Monotonicity and the Sign of the Derivative
 Monotonicity and the Sign of the Derivative
Monotonicity and the Sign of the Derivative
Looking at the graph of a function, we usually see parts where the
graph is "going up" and other parts where it is "going down".
These behaviors can be made precise in the following way: We say
that a function f(x) is increasing on an interval Iiff for any
![]()
 |
Similarly, we will say that
f(x) is decreasing on I iff for any
![]()
These two properties of a function are closely related to the
behavior of the derivative of the function (when it is
differentiable). Indeed, it is quite easy to see that f(x) is
increasing on I iff for any
![]()
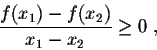
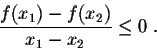
Using the Mean Value Theorem and the above ideas, we get the following powerful result:
Let f(x) be a continuous function on an arbitrary interval I and differentiable on its interior. Then
|
Remark. The practical difficulty you may encounter in using this result stems from the fact that you have to solve inequalities to determine the sign of the derivative. Consult our section on Solving Inequalities if you run into problems.
Here is a piece of advice: If the derivative is a product of functions, use the product rule for the derivative rather than multiplying out first!
Example. Consider the function

 |
From the graph, we see that the points x=-1 and x=2 are special. Indeed, at x=-1 the function behaves like a point at the top of a hill while at x=2 the graph looks like a valley. We will discuss this more on the next pages.
Exercise 1. Find the intervals on which
Exercise 2. Find the intervals on which
![]() is increasing or decreasing.
is increasing or decreasing.
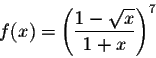
is increasing or decreasing.
 S.O.S MATHematics home page
S.O.S MATHematics home page
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA