The Pinching or Sandwich Theorem

As a motivation let us consider the function

$\begin{displaymath}f(x) = x^2 \sin\left(\frac{1}{x}\right)\;\cdot\end{displaymath}$

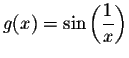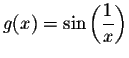When x get closer to 0, the function $\displaystyle g(x)=\sin\left(\frac{1}{x}\right)$ fails to have a limit. So we are not able to use the basic properties discussed in the previous pages. But we know that this function $\displaystyle g(x)=\sin\left(\frac{1}{x}\right)$ is bounded below by -1 and above by 1, i.e.

$\begin{displaymath}-1 \leq \sin\left(\frac{1}{x}\right) \leq 1\end{displaymath}$

for any real number x. Since $x^2 \geq 0$ , we get

$\begin{displaymath}- x^2 \leq x^2\;\sin\left(\frac{1}{x}\right) \leq x^2 \;. \end{displaymath}$

Hence when x get closer to 0, x² and -x² become very small in magnitude. Therefore any number in between will also be very small in magnitude. In other words, we have

$\begin{displaymath}\lim_{x \rightarrow 0}\quad x^2\;\sin\left(\frac{1}{x}\right) = 0\;.\end{displaymath}$

This is an example for the following general result:

Theorem: The "Pinching" or "Sandwich" Theorem Assume that

$\begin{displaymath}h(x) \leq f(x) \leq g(x)\end{displaymath}$

for any x in an interval around the point a. If

$\begin{displaymath}\lim_{x \rightarrow a} h(x) = L\;\; \mbox{and}\;\; \lim_{x \rightarrow a} g(x)= L\;,\end{displaymath}$

then

$\begin{displaymath}\lim_{x \rightarrow a} f(x) = L\;.\end{displaymath}$

Example. Let f(x) be a function such that $\vert f(x)\vert \leq M$ , for any $x \neq 0$ . The Sandwich Theorem implies

$\begin{displaymath}\lim_{x \rightarrow 0} x\;f(x) = 0\;.\end{displaymath}$

Indeed, we have

$\begin{displaymath}\vert x\; f(x)\vert \leq M \vert x\vert\end{displaymath}$

which implies

$\begin{displaymath}-M \vert x\vert \leq x\; f(x) \leq M \vert x\vert \end{displaymath}$

for any $x \neq 0$ . Since

$\begin{displaymath}\lim_{x \rightarrow 0} M\;\vert x\vert = 0\;\;\mbox{and} \;\; \lim_{x \rightarrow 0} -M\;\vert x\vert = 0\;,\end{displaymath}$

then the Sandwich Theorem implies

$\begin{displaymath}\lim_{x \rightarrow 0} x\;f(x) = 0\;.\end{displaymath}$

Exercise 1. Use the Sandwich Theorem to prove that

$\begin{displaymath}\lim_{x \rightarrow a} \sqrt{x} = \sqrt{a}\end{displaymath}$

for any a > 0.

Answer.

Exercise 2. Use the Sandwich Theorem to prove that

$\begin{displaymath}\lim_{x \rightarrow 0} x \cos\left(\frac{1}{x}\right) = 0\;.\end{displaymath}$

Answer.

Exercise 3. Consider the function

$\begin{displaymath}f(x) = \left\{ \begin{array}{lll} 1 + 2x^2 &\mbox{if $x$ is r... ...\\ 1 + x^4 &\mbox{if $x$ is irrational.}\\ \end{array}\right.\end{displaymath}$

Use the Sandwich Theorem to prove that

$\begin{displaymath}\lim_{x \rightarrow 0} f(x) = 1\;.\end{displaymath}$

Answer.

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA