 Limits and Infinity
Limits and Infinity
 Limits and Infinity
Limits and Infinity
One of the mysteries of Mathematics seems to be the concept of
"infinity", usually denoted by the symbol ![]() .
So what
is
.
So what
is ![]() ? It is simply a symbol that represents large numbers.
Indeed, numbers are of three kinds: large, normal size, and
small. The normal size numbers are the ones that we have a clear
feeling for. For example, what does a trillion mean? That is a
very large number. Also numbers involved in macro-physics are very
large numbers. Small numbers are usually used in micro-physics.
Numbers like 10-75 are very small. Being positive or
negative has special meaning depending on the problem at hand. The
common mistake is to say that
? It is simply a symbol that represents large numbers.
Indeed, numbers are of three kinds: large, normal size, and
small. The normal size numbers are the ones that we have a clear
feeling for. For example, what does a trillion mean? That is a
very large number. Also numbers involved in macro-physics are very
large numbers. Small numbers are usually used in micro-physics.
Numbers like 10-75 are very small. Being positive or
negative has special meaning depending on the problem at hand. The
common mistake is to say that ![]() is smaller than 0. While
this may be true according to the natural order on the real line
in term of sizes,
is smaller than 0. While
this may be true according to the natural order on the real line
in term of sizes, ![]() is big, very big!
is big, very big!
So when do we have to deal with ![]() and
and ![]() ? Easy:
whenever you take the inverse of small numbers, you generate
large numbers and vice-versa. Mathematically we can write this
as:
? Easy:
whenever you take the inverse of small numbers, you generate
large numbers and vice-versa. Mathematically we can write this
as:
Remark. Do not treat ![]() as ordinary numbers. These
symbols do not obey the usual rules of arithmetic, for instance,
as ordinary numbers. These
symbols do not obey the usual rules of arithmetic, for instance,
![]() ,
,
![]() ,
,
![]() ,
etc.
,
etc.
Example. Consider the function
 |
Note that when x gets closer to 3, then the points on the graph get closer to the (dashed) vertical line x=3. Such a line is called a vertical asymptote. For a given function f(x), there are four cases, in which vertical asymptotes can present themselves:
 |
Next we investigate the behavior of functions when
![]() .
We have seen that
.
We have seen that
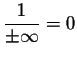 .
So for example, we have
.
So for example, we have
Example. Consider the function
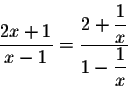
 |
Note that when x gets closer to
![]() (x gets large),
then the points on the graph get closer to the horizontal line
y=2. Such a line is called a horizontal asymptote.
(x gets large),
then the points on the graph get closer to the horizontal line
y=2. Such a line is called a horizontal asymptote.
In particular, we have
Example. Consider the function
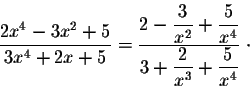
Example. Consider the function
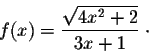

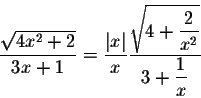


Remark. Be careful! A common mistake is to assume that
![]() .
This is true if
.
This is true if ![]() and false if x < 0.
and false if x < 0.
Exercise 1. Find
Exercise 2. Find
Exercise 3. Find
Exercise 4. Find
Exercise 5. Find the vertical and horizontal asymptotes for
the graph of
![\begin{displaymath}\lim_{x \rightarrow \infty} \sqrt[3]{\frac{x^2+3}{27x^2 -1}}\;\cdot\end{displaymath}](img38.gif)
![]()
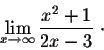
![]()
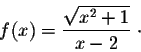
 S.O.S MATHematics home page
S.O.S MATHematics home page
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA